题目内容
 如图,D、E是△ABC边上两点,且DE∥BC.若△ADE与△BCE的面积分别为2与12,则△ABC的面积为________.
如图,D、E是△ABC边上两点,且DE∥BC.若△ADE与△BCE的面积分别为2与12,则△ABC的面积为________.
18
分析:设S△BDE=x,则可得出△ABE、△BCE的面积之比,再将x的值代入即可得出答案.
解答: 解:(1)设S△BDE=x.
解:(1)设S△BDE=x.
∴ =
=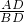 ,
,
∴ =
= .
.
∵DE∥BC,
∴△ADE∽△ABC,
∴ =
= ,
,
∴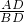 =
= ,
,
∵S△ADE=2,S△BCE=12,
∴ =
= ,
,
解得:x1=-6(舍),x2=4.
∴S△BDE=4,
∴△ABC的面积为:12+2+4=18.
故填:18.
点评:本题考查了平行线分线段成比例定理以及分式方程的应用,难度较大.
分析:设S△BDE=x,则可得出△ABE、△BCE的面积之比,再将x的值代入即可得出答案.
解答:
 解:(1)设S△BDE=x.
解:(1)设S△BDE=x.∴
 =
=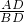 ,
,∴
 =
= .
.∵DE∥BC,
∴△ADE∽△ABC,
∴
 =
= ,
,∴
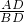 =
= ,
,∵S△ADE=2,S△BCE=12,
∴
 =
= ,
,解得:x1=-6(舍),x2=4.
∴S△BDE=4,
∴△ABC的面积为:12+2+4=18.
故填:18.
点评:本题考查了平行线分线段成比例定理以及分式方程的应用,难度较大.

练习册系列答案
相关题目


 20、已知:如图,E、F是AB上的两点,AE=BF,AC∥BD,∠C=∠D.求证:CF=DE.
20、已知:如图,E、F是AB上的两点,AE=BF,AC∥BD,∠C=∠D.求证:CF=DE. (2013•荣昌县模拟)如图,⊙O的直径是AB,∠C=35°,则∠DAB的度数是( )
(2013•荣昌县模拟)如图,⊙O的直径是AB,∠C=35°,则∠DAB的度数是( )