��Ŀ����
����Ŀ���Ķ����в��ϣ������Ӧ������ȫ���ı��θ���ȫ��ͼ�εĶ��ֿ�֪:�����߷ֱ���ȡ��ĸ���Ҳ�ֱ���ȵ������ı���ȫ�ȡ��ڡ�̽��������ȫ�ȵ�������ʱ�����ǰ������������С�һ���ߺ͵ȡ���һ������ȡ���Ϊһ������.�ǻ�С���ͬѧ��ȡ�̽��������ȫ���������ķ���̽�����ı���ȫ�ȵ�������������������˼��:��ͼ1���ı���![]() ���ı���
���ı���![]() �У����ӶԽ���
�У����ӶԽ���![]() �����������ı���ȫ�ȵ������ת��Ϊ��
�����������ı���ȫ�ȵ������ת��Ϊ��![]() ���롰
���롰![]() �������⡣���ȸ�����
�������⡣���ȸ�����![]() ����������ֻҪ������
����������ֻҪ������![]() ������ʹ��
������ʹ��![]() �������Ƴ������ı����С������߷ֱ���ȡ��ĸ���Ҳ�ֱ�͵ȡ����Ӷ�˵�������ı���ȫ�ȡ�
�������Ƴ������ı����С������߷ֱ���ȡ��ĸ���Ҳ�ֱ�͵ȡ����Ӷ�˵�������ı���ȫ�ȡ�
�����ǻ�С���˼·��С����ͼ![]() �е��ı���
�е��ı���![]() ���ı���
���ı���![]() �ȸ�����������:
�ȸ�����������: ![]() ,
,![]() ��С���ڴ˻������ָ�����
��С���ڴ˻������ָ�����![]() ����������.������Ϊ��������������ܵõ����ı���
����������.������Ϊ��������������ܵõ����ı���![]() �ı���
�ı���![]() ��.
��.

��1�������С����С��������������˵�����ı���![]() �ı���
�ı���![]() �������ɣ�
�������ɣ�
��2���������![]() ��������ѡһ��������ѡ�� ��.
��������ѡһ��������ѡ�� ��.
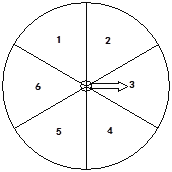
![]() �ڲ����С�С�������������Ļ����ϣ�Сӱ�ָ�������������
�ڲ����С�С�������������Ļ����ϣ�Сӱ�ָ�������������![]() ��.������������� ����ܡ����ܡ����õ��ı���
��.������������� ����ܡ����ܡ����õ��ı���![]() �ı���
�ı���![]()
![]() �ڲ����С�С�����������Ļ����ϡ�����������������ԭ�ı��ε�������Ҫ��ͬ��С������������ʹ�ı���
�ڲ����С�С�����������Ļ����ϡ�����������������ԭ�ı��ε�������Ҫ��ͬ��С������������ʹ�ı���![]() �ı���
�ı���![]() �������ӵ������Ǣ� ���� .
�������ӵ������Ǣ� ���� .
���𰸡���1�������� ����2��A��B��A������ B����![]() ����
����![]() ��
��
��������
��1������ȫ�������ε����ʺ��ж�������⣬���ɵõ��ı���![]() �ı���
�ı���![]() ����2�����������ε��жϺ����ʣ����ɵõ���.
����2�����������ε��жϺ����ʣ����ɵõ���.
![]() ����ɵã�
����ɵã�![]()
![]()
��![]()
![]()
![]()
![]()
![]() ��
��![]()
![]() �ı���
�ı���![]() �ı���
�ı���![]()
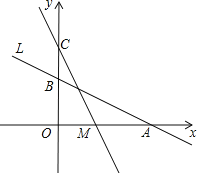
![]() A�����ܣ����жϵڶ���������ȫ�ȣ�
A�����ܣ����жϵڶ���������ȫ�ȣ�
B��![]() ��
��![]() ���𰸲�Ψһ�����ж�
���𰸲�Ψһ�����ж�![]() ���ɣ�
���ɣ�

 ������������Ӧ����ϵ�д�
������������Ӧ����ϵ�д� ͬ����չ�Ķ�ϵ�д�
ͬ����չ�Ķ�ϵ�д�����Ŀ��ijУΪ�˽�2014����꼶ѧ�������鼮������������������ȡ��50��ѧ�������鼮�����������ͳ�ƽ���г����µı������Ƴ���ͼ��ʾ������ͳ��ͼ�����п��������ռ��50��ѧ�������ܲ�����40%��
��� | ������ | �̸��� | ������ | ���� |
���������� | 168 | 105 | m | 32 |
��1����������ĸm��ֵ���� ��
��2������ͳ��ͼ�����̸���������Ӧ��Բ�Ľ����Ķ���Ϊ ����
��3����У2014����꼶��600��ѧ����������Ƹ��꼶ѧ�������Ľ̸����鼮Լ���ٱ���