题目内容
5.解方程组:$\left\{\begin{array}{l}{3x+2y+z=13}\\{x+y+2z=7}\\{2x-3y+z=12}\end{array}\right.$.分析 ①×2-②得出5x+3y=19④,①-③得出x+5y=1⑤,由④和⑤组成一个二元一次方程组,求出方程组的解,把x、y的值代入②求出z即可.
解答 解:$\left\{\begin{array}{l}{3x+2y+z=13①}\\{x+y+2z=7②}\\{2x-3y+z=12③}\end{array}\right.$
①×2-②得:5x+3y=19④,
①-③得:x+5y=1⑤,
由④和⑤组成一个二元一次方程组:$\left\{\begin{array}{l}{5x+3y=19}\\{x+5y=1}\end{array}\right.$
解得:x=$\frac{46}{11}$,y=-$\frac{7}{11}$,
把=$\frac{46}{11}$,y=-$\frac{7}{11}$代入②得:$\frac{46}{11}$-$\frac{7}{11}$+2z=7,
解得:z=$\frac{19}{11}$,
所以原方程组的解为:$\left\{\begin{array}{l}{x=\frac{46}{11}}\\{y=-\frac{7}{11}}\\{z=\frac{19}{11}}\end{array}\right.$.
点评 本题考查了解三元一次方程组和解二元一次方程组的应用,解此题的关键是能把三元一次方程组转化成二元一次方程组,难度适中.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
16.现规定:f(x)=8x5-12x4+6x3.若M(x)=f(x)÷(-2x2),则M(-2)的值为( )
| A. | -2 | B. | -14 | C. | 60 | D. | 62 |
13.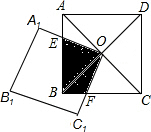 如图,正方形ABCD的对角线交于点O,点O又是正方形A1B1C1O的一个顶点,而且这两个正方形的边长相等.无论正方形A1B1C1O绕点O怎样转动,两个正方形重叠部分的面积,总等于一个正方形面积的( )
如图,正方形ABCD的对角线交于点O,点O又是正方形A1B1C1O的一个顶点,而且这两个正方形的边长相等.无论正方形A1B1C1O绕点O怎样转动,两个正方形重叠部分的面积,总等于一个正方形面积的( )
 如图,正方形ABCD的对角线交于点O,点O又是正方形A1B1C1O的一个顶点,而且这两个正方形的边长相等.无论正方形A1B1C1O绕点O怎样转动,两个正方形重叠部分的面积,总等于一个正方形面积的( )
如图,正方形ABCD的对角线交于点O,点O又是正方形A1B1C1O的一个顶点,而且这两个正方形的边长相等.无论正方形A1B1C1O绕点O怎样转动,两个正方形重叠部分的面积,总等于一个正方形面积的( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{5}$ |