题目内容
如图,在Rt△ABC中,∠ACB=90º,∠B=30º,将△ABC绕点C按顺时针方向旋转n度后,得到△DEC,点D刚好落在AB边上.
(1)求n的值;
(2)若F是DE的中点,判断四边形ACFD
的形状,并说明理由.
 |
解:(1)由旋转可知,CA=CD.
∵∠ACB=90º,∠B=30º,∴∠A=60º.
∴△ACD为等边三角形.∴∠ACD=60º,即n=60.
(2)四边形ACFD是菱形.
理由:∵F是DE的中点, ∴ .
.
∵∠EDC=∠A=60º, ∴△FCD为等边三角形, ∴ .
.
∵△ACD为等边三角形. ∴ .
.
∴ . ∴四边形ACFD是菱形. -
. ∴四边形ACFD是菱形. -
(说明:此题说理方法较多,如可以先说明是平行四边形再说明邻边,等)

练习册系列答案
相关题目
科学家为了推测最适合某种珍奇植物生长的温度,将这种植物分别放在不同温度的环境中,经过一定时间后,测试出这种植物高度的增长
 情况,部分数据如下表:
情况,部分数据如下表:
| 温度t/℃ | -4 | -2 | 0 | 1 | 4 |
| 植物高度增长量l/mm | 41 | 49 | 49 | 46 | 25 |
科学家经过猜想、推测出l与t之间是二次函数关系.由
此可以推测最适合这种植物生长的温度为 ℃.

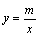 与直线
与直线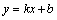 相交于点M,N,且点M的坐标为(1,3),点N的纵坐标为
相交于点M,N,且点M的坐标为(1,3),点N的纵坐标为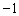 .根据图象信息可得关于x的方程
.根据图象信息可得关于x的方程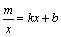 的解为( )
的解为( )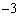 ,1 B.
,1 B.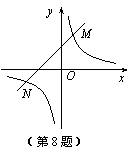
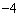 ,4).点P从点A出发,以每秒1个单位长度的速度沿x轴向点O运动;点Q从点O同时出发,以相同的速度沿x轴的正方向运动,规定点P到达点O时,点Q也停止运动.连接BP,过P点作BP的垂线,与过点Q平行于y轴的直线l相交于点D.BD与
,4).点P从点A出发,以每秒1个单位长度的速度沿x轴向点O运动;点Q从点O同时出发,以相同的速度沿x轴的正方向运动,规定点P到达点O时,点Q也停止运动.连接BP,过P点作BP的垂线,与过点Q平行于y轴的直线l相交于点D.BD与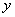 轴交于点E,连接PE.设点P运动的时间为t(s).
轴交于点E,连接PE.设点P运动的时间为t(s).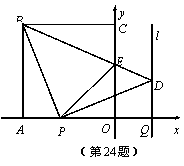
 的解集在数轴上表示为【 】
的解集在数轴上表示为【 】 B.
B. C.
C. D.
D.
 平方米,预计到明年年底的绿化面积将会增加到
平方米,预计到明年年底的绿化面积将会增加到 平方米,求这两年的年平均增长率。
平方米,求这两年的年平均增长率。