题目内容

若A为锐角，且tanA=2，求 $数学公式$ ．

解：

如图，∵在Rt△ACB中，∠C=90°，tanA= $\text{[math]}$ ，sinA= $\text{[math]}$ ，cosA= $\text{[math]}$ ，
∴ $\text{[math]}$ = $\text{[math]}$ = $\text{[math]}$ ，
∴tanA= $\text{[math]}$ ，
∵tanA=2，
∴ $\text{[math]}$ =tanA=2，
∴ $\text{[math]}$
= $\text{[math]}$
= $\text{[math]}$
= $\text{[math]}$
=- $\text{[math]}$ ．
分析：求出tanA= $\text{[math]}$ ，分式的分子和分母都除以cosA，把tanA= $\text{[math]}$ 代入求出即可．
点评：本题考查了解直角三角形和勾股定理的应用，注意：tanA= $\text{[math]}$ ．

练习册系列答案

中考说明与训练系列答案

中考备考每天一点系列答案

征服英语名师课时计划系列答案

考前系列答案

口算心算快速算系列答案

跨越中考总复习方略系列答案

新语文阅读训练系列答案

秒杀口算题系列答案

口算题卡加应用题集训系列答案

中考1加1系列答案

相关题目

若α为锐角，且tanα=

，则有（　　）

A、0°＜α＜30°

B、30°＜α＜45°

C、45°＜α＜60°

D、60°＜α＜90°

若∠α为锐角，且tanα＞

，则α的取值范围是（　　）

A、60°＜α＜90°

B、30°＜α＜60°

C、45°＜α＜60°

（2013•常州模拟）（1）请在一个3×2的矩形网格里（每个小正方形的边长都是1），画出一个以格点为顶点的等腰直角三角形，使其直角边长为

，并适当加以文字说明．
（2）借助上述图形，解释下列结论：
若α与β为锐角，且tanα=

，则α+β=45°．
（3）构造几何图形，解释下列结论：
若α与β为锐角，且tanα=

，其中a＞b＞0，则α+β=45°．

若α为锐角，且tanα=，则有（??? ）

A．0°＜α＜30°??? B．30°＜α＜45°

C．45°＜α＜60°?? D．60°＜α＜90°

（1）请在一个3×2的矩形网格里（每个小正方形的边长都是1），画出一个以格点为顶点的等腰直角三角形，使其直角边长为 $数学公式$ ，并适当加以文字说明．
（2）借助上述图形，解释下列结论：
若α与β为锐角，且tanα= $数学公式$ ，tanβ= $数学公式$ ，则α+β=45°．
（3）构造几何图形，解释下列结论：
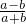若α与β为锐角，且tanα= $数学公式$ ，tanβ= $数学公式$ ，其中a＞b＞0，则α+β=45°．