题目内容
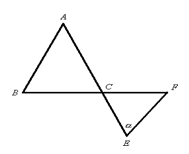
如图，AE与BF交于C，且AB=AC，CE=CF．∠E=α．那么，∠A用α可以表示成
- A.180°-α
- B.180°-4α
- C.2α-180°
- D.4α-180°
D
分析：根据等腰三角形的性质和三角形内角和定理可求∠ECF的度数，再根据对顶角相等、等腰三角形的性质和三角形内角和定理可求∠A的度数．
解答：∵CE=CF，∠E=α，
∴∠F=α，
∴∠ECF=180°-2α，
∴∠ACB=180°-2α，
∵AB=AC，
∴∠B=180°-2α，
∴∠A=4α-180°．
故选D．
点评：考查了等腰三角形的性质和三角形内角和定理，注意两个三角形可以通过对顶角相等解题．
分析：根据等腰三角形的性质和三角形内角和定理可求∠ECF的度数，再根据对顶角相等、等腰三角形的性质和三角形内角和定理可求∠A的度数．
解答：∵CE=CF，∠E=α，
∴∠F=α，
∴∠ECF=180°-2α，
∴∠ACB=180°-2α，
∵AB=AC，
∴∠B=180°-2α，
∴∠A=4α-180°．
故选D．
点评：考查了等腰三角形的性质和三角形内角和定理，注意两个三角形可以通过对顶角相等解题．
练习册系列答案
相关题目
21、如图，在正方形ABCD中，E、F分别为BC、CD边上的点，CE=DF，AE与BF交于点M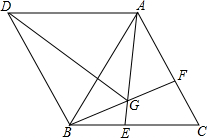
如图，△ABC与△ABD都是等边三角形，点E，F分别在BC，AC上，BE=CF，AE与BF交于点G．
如图，AE与BF交于C，且AB=AC，CE=CF．∠E=α．那么，∠A用α可以表示成（ ）
．那么，∠A用