题目内容
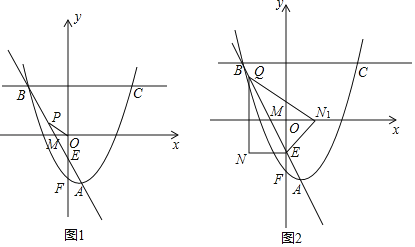
【题目】已知抛物线C1:y=ax2﹣4ax﹣5的开口向上.
(1)当a=1时,求抛物线与x轴的交点坐标;
(2)试说明抛物线C1一定经过两个定点,并求出这两个定点的坐标;
(3)将抛物线C1沿(2)所求的两个定点所在直线翻折,得到抛物线C2,
①写出抛物线C2的表达式;
②当抛物线C2的顶点到x轴的距离为2,求a的值.
【答案】(1)抛物线与x轴的交点坐标为(﹣1,0)或(5,0);(2)抛物线C1一定经过两个定点(0,﹣5),(4,﹣5);(3)①抛物线C2解析式为y=﹣ax2+4ax﹣5,②a=![]() 或
或![]() .
.
【解析】
(1)将a=1代入函数解析式,即可求出函数的解析式,然后令y=0,求出x的值即可解决.
(2)将解析式化成两部分,一部分为常数项,另一部分进行因式分解写成几个因式相乘的形式,观察解析式的特征,即可解决问题.
(3)①根据翻折的性质,抛物线开口方向相反,但对称轴没有发生变化,根据此可以得到抛物线C2解析式为:y=﹣ax2+4ax﹣5,②根据二次函数的性质,可知y=2或y=-2,对称轴未发生变化,x=2,将两者分别代入,求出a的值即可.
(1)当a=1时,抛物线解析式为y=x2﹣4x﹣5=(x﹣2)2﹣9,
∴对称轴为x=2;
∴当y=0时,x﹣2=3或﹣3,即x=﹣1或5;
∴抛物线与x轴的交点坐标为(﹣1,0)或(5,0);
(2)抛物线C1解析式为:y=ax2﹣4ax﹣5,
整理得:y=ax(x﹣4)﹣5;
∵当ax(x﹣4)=0时,y恒定为﹣5;
∴抛物线C1一定经过两个定点(0,﹣5),(4,﹣5);
(3)①这两个点连线为y=﹣5;
将抛物线C1沿y=﹣5翻折,得到抛物线C2,开口方向变了,但是对称轴没变;
∴抛物线C2解析式为:y=﹣ax2+4ax﹣5,
②抛物线C2的顶点到x轴的距离为2,
则x=2时,y=2或者﹣2;
当y=2时,2=﹣4a+8a﹣5,解得,a=![]() ;
;
当y=﹣2时,﹣2=﹣4a+8a﹣5,解得,a=![]() ;
;
∴a=![]() 或
或![]() .
.

【题目】为了解某校初三学生上周末使用手机的情况(选项:A.聊天;B.学习;C.购物;D.游戏;E.其他),随机抽查了该校初三若干名学生,对其上周末使用手机的情况进行统计(每个学生只选一个选项),绘制了统计表和条形统计图.
选项 | 人数 | 频率 |
A | 15 | 0.3 |
B | 10 | m |
C | 5 | 0.1 |
D | n | |
E | 5 | 0.1 |
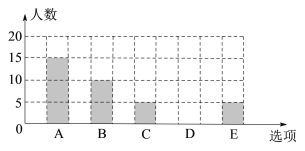
根据以上信息回答下列问题:
(1)这次调查的样本容量是 ;
(2)统计表中m= ,n= ,补全条形统计图;
(3)若该校初三有540名学生,请估计该校初三学生上周末利用手机学习的人数.