题目内容
17. 如图,抛物线y=ax2-$\frac{3}{2}$x-2(a≠)的图象与x轴交于A、B两点,与y轴交于C点,已知B点坐标为(4,0).
如图,抛物线y=ax2-$\frac{3}{2}$x-2(a≠)的图象与x轴交于A、B两点,与y轴交于C点,已知B点坐标为(4,0).(1)求抛物线的解析式;
(2)若点M是线段BC下方的抛物线上一点,求△MBC的面积的最大值,并求出此时M点的坐标;
(3)试探究:△ABC的外接圆的圆心位置,并求出圆心坐标.
分析 (1)该函数解析式只有一个待定系数,只需将B点坐标代入解析式中即可.
(2)利用过点M作y轴的平行线,再利用S△MBC=S△CME+S△BEM得出二次函数最值得出答案;
(3)首先根据抛物线的解析式确定A点坐标,然后通过证明△ABC是直角三角形来推导出直径AB和圆心的位置,由此确定圆心坐标.
解答 解:(1)将B(4,0)代入抛物线的解析式中,得:
0=16a-$\frac{3}{2}$×4-2,即:a=$\frac{1}{2}$;
∴抛物线的解析式为:y=$\frac{1}{2}$x2-$\frac{3}{2}$x-2.
(2)可得:B(4,0)、C(0,-2),设直线BC的解析式为:y=kx+b,
则$\left\{\begin{array}{l}{4k+b=0}\\{b=-2}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=1}\\{b=-2}\end{array}\right.$
故直线BC的解析式为:y=x-2;
设xM=t,则yM=$\frac{1}{2}$t2-$\frac{3}{2}$t-2,yN=$\frac{1}{2}$t-2,
S△MBC=S△CME+S△BEM=$\frac{1}{2}$EM•ON+$\frac{1}{2}$EM•BN=$\frac{1}{2}$EM•OB
=$\frac{1}{2}$($\frac{1}{2}$t-2-$\frac{1}{2}$t2+$\frac{3}{2}$t+2)×4
=-t2+4t
=-(t-2)2+4,
∴当t=2时,S△MBC=最大值为4,此时M(2,-3);
(3)由(1)的函数解析式可求得:A(-1,0)、C(0,-2);
∴OA=1,OC=2,OB=4,
即:OC2=OA•OB,
又∵OC⊥AB,
∴△OAC∽△OCB,
∴∠OCA=∠OBC;
∴∠ACB=∠OCA+∠OCB=∠OBC+∠OCB=90°,
∴△ABC为直角三角形,AB为△ABC外接圆的直径;
∴该外接圆的圆心为AB的中点,且坐标为(1.5,0).
点评 此题考查了二次函数综合题,熟练掌握待定系数法求函数解析式、二次函数最值求法以及三角形的面积公式,正确利用相似三角形的性质解题是关键.

 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
 下列俯视图正确的是( )
下列俯视图正确的是( )| A. |  | B. |  | C. |  | D. |  |
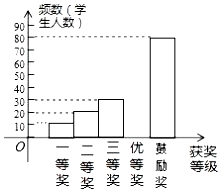 为了进一步普及足球知识,传播足球文化,某市举行了“足球进校园”知识竞赛活动,为了解足球知识的普及情况,随机抽取了部分获奖情况进行整理,得到下列不完整的统计图表:
为了进一步普及足球知识,传播足球文化,某市举行了“足球进校园”知识竞赛活动,为了解足球知识的普及情况,随机抽取了部分获奖情况进行整理,得到下列不完整的统计图表:| 获奖等次 | 频数 | 频率 |
| 一等奖 | 10 | 0.05 |
| 二等奖 | 20 | 0.10 |
| 三等奖 | 30 | b |
| 优胜奖 | a | 0.30 |
| 鼓励奖 | 80 | 0.40 |
(1)a=60,b=0.15;
(2)补全频数分布直方图;
(3)在这次竞赛中,甲、乙、丙、丁四位同学都获得一等奖,若从这四位同学中随机选取两位同学代表该市参加上一级竞赛,请用树状图或列表的方法,计算恰好选中甲、乙二人的概率.
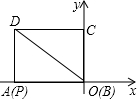 如图,在平面直角坐标系中,矩形ABCD的边AB,BC分别在x轴,y轴上,点D在第二象限,AB=8,BC=6,矩形ABCD沿OD方向以每秒1个单位长度的速度运动.同时点P从点A出发沿折线AD-DC以每秒1个单位长度向终点C运动,当点P到达点C时,矩形ABCD也停止运动,设点P的运动时间为r(s),△PDo的面积为S(平方单位),
如图,在平面直角坐标系中,矩形ABCD的边AB,BC分别在x轴,y轴上,点D在第二象限,AB=8,BC=6,矩形ABCD沿OD方向以每秒1个单位长度的速度运动.同时点P从点A出发沿折线AD-DC以每秒1个单位长度向终点C运动,当点P到达点C时,矩形ABCD也停止运动,设点P的运动时间为r(s),△PDo的面积为S(平方单位),