Question

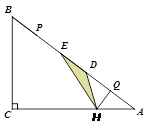
如图，Rt△ABC中，∠C=90°，BC=6，AC=8．点P，Q都是斜边AB上的动点，点P从B 向A运动（不与点B重合），点Q从A向B运动，BP=AQ．点D，E分别是点A，B以Q，P为对称中心的对称点， HQ⊥AB于Q，交AC于点H．当点E到达顶点A时，P，Q同时停止运动．设BP的长为x，△HDE的面积为y．

（1）求证：△DHQ∽△ABC；

（2）求y关于x的函数解析式并求y的最大值；

 

Answer 1

 

（1）证明略

（2）

解析:解：

（1）∵A、D关于点Q成中心对称，HQ⊥AB，

∴=90°，HD=HA，

∴，

∴△DHQ∽△ABC． …………………………………………………………2分

（2）①如图1，当时，

ED=，QH=，

此时．…………………………………………3分

当时，最大值．………………………………………………………4分

②如图2，当时，

ED=，QH=，

此时．………………………………5分

当时，最大值．……………………………………………6分

∴y与x之间的函数解析式为

∴y的最大值是．………………………………………………………8分