题目内容
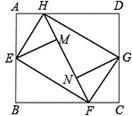
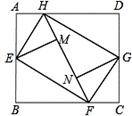
将矩形纸张ABCD四个角向内折起恰好拼成一个既无缝隙又无重叠的四边形EFGH,若EH=5,EF=12,则矩形ABCD的面积为
A.30 B.60 C.120 D.240
【答案】
C
【解析】
试题分析:根据折叠的性质可得∠HEF=∠EFG=∠FGH=∠GHE=90°,所以可判断四边形EHFG是矩形,再由矩形ABCD的面积等于矩形HEFG的面积的2倍,可得出答案.
由题意得,∠HEM=∠HEA,∠MEF=∠BEF,
则∠HEF=∠HEM+∠MEF ∠AEB=90°,
∠AEB=90°,
同理可得:∠HEF=∠EFG=∠FGH=∠GHE=90°,
即可得四边形EHFG是矩形,其面积=EH×EF=5×12=60,
由折叠的性质可得:矩形ABCD的面积等于矩形HEFG的面积的2倍=2×60=120,
故选C.
考点:折叠的性质,矩形的面积公式
点评:解题的关键是判断四边形EHFG是矩形,得出矩形ABCD的面积等于矩形HEFG的面积的2倍.

练习册系列答案
相关题目
将矩形纸张ABCD四个角向内折起恰好拼成一个既无缝隙又无重叠的四边形EFGH,若EH=5,EF=12,则矩形ABCD的面积为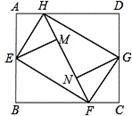
| A.30 | B.60 | C.120 | D.240 |