题目内容
3. 已知在Rt△ABC中,BC=6,CD是斜边AB上的中线,点G是△ABC的重心,将△ADC绕重点G旋转,得到△A1D1C1,并且C1D1∥AB,直线A1D1⊥AC,设直线A1C1、A1D1分别交AC于点E,F,那么EF的长为$\frac{5\sqrt{3}}{3}$或3$\sqrt{3}$.
已知在Rt△ABC中,BC=6,CD是斜边AB上的中线,点G是△ABC的重心,将△ADC绕重点G旋转,得到△A1D1C1,并且C1D1∥AB,直线A1D1⊥AC,设直线A1C1、A1D1分别交AC于点E,F,那么EF的长为$\frac{5\sqrt{3}}{3}$或3$\sqrt{3}$.
分析 分两种情形:①如图1中,延长C1D1交AC于M.只要证明∠A=30°,求出AC、AB、CC1、EC1/、A1E即可解决问题.②如图2中,在Rt△EFD1中,因为∠EFD1=90°,ED1=6,∠FED1=30°,根据cos30°=$\frac{EF}{E{D}_{1}}$,即可计算.
解答 解:①如图1中,延长C1D1交AC于M.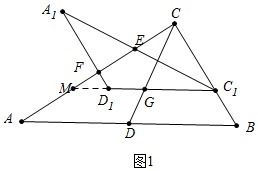
∵∠ACB=90°,AD=DB,
∴∠DAC=∠DCA=∠A1=∠A1C1M,
∵C1M∥AB,
∴∠A=∠EMC1=∠A1C1M,
∴∠A1EF=∠EMG+∠EC1M=2∠CMG=2∠A1,
∵A1D1⊥AC,
∴∠A1FE=90°,
∴∠A1=30°,∠A1EF=∠CEC1=60°,
在Rt△ABC中,∵∠ACB=90°,∠A=30°BC=6,
∴AB=2AC=12,AC=A1C1=$\sqrt{A{B}^{2}-B{C}^{2}}$=6$\sqrt{3}$,
∵GC1∥DB,
∴$\frac{CG}{GD}$=$\frac{C{C}_{1}}{B{C}_{1}}$=2,
∴CC1=4,
在Rt△ECC1中,∵∠ECC1=90°,∠CEC1=60°,
∴sin60°=$\frac{C{C}_{1}}{E{C}_{1}}$,
∴EC1=$\frac{8\sqrt{3}}{3}$,
∴A1E=6$\sqrt{3}$-$\frac{8\sqrt{3}}{3}$=$\frac{10\sqrt{3}}{3}$,
在Rt△A1EF中,∵∠A1FE=90°,∠A1=30°,
∴EF=$\frac{1}{2}$A1E=$\frac{5\sqrt{3}}{3}$.
②如图2中,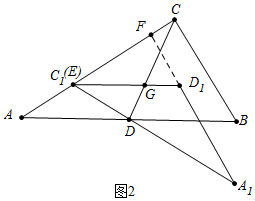
同理可证∠A=∠A1=∠FEG=30°,
在Rt△EFD1中,∵∠EFD1=90°,ED1=6,∠FED1=30°,
∴cos30°=$\frac{EF}{E{D}_{1}}$,
∴EF=3$\sqrt{3}$,
综上所述,EF的长为$\frac{5\sqrt{3}}{3}$或3$\sqrt{3}$.
故答案为$\frac{5\sqrt{3}}{3}$或3$\sqrt{3}$.
点评 本题考查旋转变换、三角形的重心、直角三角形斜边中线的性质、平行线的性质、直角三角形30度角性质、勾股定理等知识,解题的关键是发现特殊角30°,注意学会分类讨论,不能漏解,属于中考填空题中的压轴题.

 名校课堂系列答案
名校课堂系列答案 如图,CD是AB的垂直平分线,AC=1.6cm,BD=2.4cm,则四边形ACBD的周长为( )
如图,CD是AB的垂直平分线,AC=1.6cm,BD=2.4cm,则四边形ACBD的周长为( )| A. | 4cm | B. | 8cm | C. | 5.6cm | D. | 6.4cm |
| A. | 3个 | B. | 4个 | C. | 5个 | D. | 6个 |
| A. | -6 | B. | 6 | C. | -$\frac{1}{6}$ | D. | $\frac{1}{6}$ |


 直线y=x+6交x轴、y轴于A、B两点,AC⊥AB交y轴于C,P为x轴正半轴上一点.
直线y=x+6交x轴、y轴于A、B两点,AC⊥AB交y轴于C,P为x轴正半轴上一点. 如图,EF∥AD,∠1=∠2,∠BAC=70°,
如图,EF∥AD,∠1=∠2,∠BAC=70°,