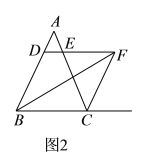��Ŀ����
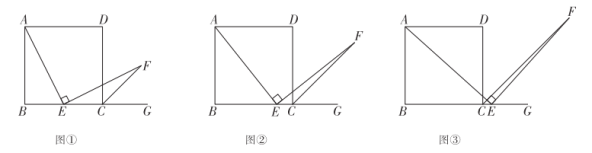
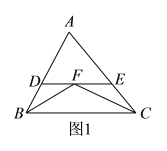
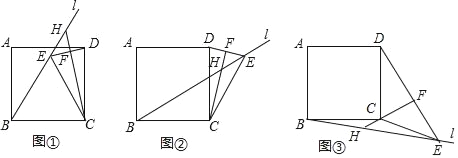
����Ŀ����������ABCD�У�����B��ֱ��l����E��ֱ��l�ϣ�����CE��DE��CE=BC������C��CF��DE�ڵ�F����ֱ��l�ڵ�H����l����ͼ����λ��ʱ����֤��BH+EH=![]() CH������֤������
CH������֤������
��1����l����ͼ����λ��ʱ���߶�BH��EH��CH֮����������������ϵ��д����IJ��룬������֤����
��2����l����ͼ����λ��ʱ���߶�BH��EH��CH֮����������������ϵ��д����IJ��룬����֤����
���𰸡���1��BH��EH=![]() CH��2��EH��BH=
CH��2��EH��BH=![]() CH
CH
������������: ��1�����жϳ���BCG=��ECG=![]() ��BCE�����жϳ���ECF=��DCF=
��BCE�����жϳ���ECF=��DCF=![]() ��DCE���ó���GCH=��GCE-��ECF=
��DCE���ó���GCH=��GCE-��ECF=![]() ����BCE-��DCE��=45�㣬������CGH�ǵ���ֱ�������Σ������ó�CH=
����BCE-��DCE��=45�㣬������CGH�ǵ���ֱ�������Σ������ó�CH=![]() GH�����жϳ�BG=EG=
GH�����жϳ�BG=EG=![]() BE���ɵó����ۣ�
BE���ɵó����ۣ�
��2��ͬ��1���ķ������ɵó����ۣ�
���:
��1��BH��EH=![]() CH��
CH��
�������£�
����C��CG��BH��G��
��ͼ����ʾ��
���ı���ABCD�������Σ�
��CB=CD����BCD=90�㣬
��CE=CB��
���BCG=��ECG=![]() ��BCE��
��BCE��
��CE��DE��CD=CB=CE��
���ECF=��DCF=![]() ��DCE��
��DCE��
���GCH=��GCE����ECF=![]() ����BCE����DCE��=45��
����BCE����DCE��=45��
���CGH�ǵ���ֱ�������Σ�
��CH=![]() GH��
GH��
��CB=CE��CG��BE��
��BG=EG=![]() BE��
BE��
��BH��EH=BG+GH��EH=BG+EG��EH��EH=2GH=![]() CH
CH
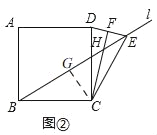
��2�����룺EH��BH=![]() CH��
CH��
���ɣ���ͼ�ۣ�����C��CG��BE��G��
ͬ��1���ã���CGH�ǵ���ֱ�������Σ�
CH=![]() GH��
GH��
��CB=CE��CG��BE��
��BG=EG=![]() BE��
BE��
��EH��BH=HG+GE����BG��HG��=2HG=![]() CH��
CH��
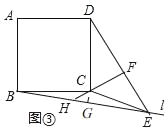
�㾦: �������ı����ۺ��⣬��Ҫ�����������ε����ʡ���ת�����ʡ����������ε����ʡ�����ֱ�������ε��ж������ʵ�֪ʶ�������GCH=45���ǽⱾ��Ĺؼ�.

 �����������һ��һ��ϵ�д�
�����������һ��һ��ϵ�д� Ӧ������ҵ��ϵ�д�
Ӧ������ҵ��ϵ�д�