题目内容
若△ABC中,AB=13cm,AC=15cm,高AD=12,则△ABC的周长为 cm.
考点:勾股定理
专题:
分析:在直角△ACD与直角△ABD中,根据勾股定理即可求得BD,CD的长,得到BC的长.即可求解.
解答: 解:直角△ACD中:CD=
解:直角△ACD中:CD=
=
=9cm;
在直角△ABD中:BD=
=
=5cm.
当D在线段BC上时,如图(1):BC=BD+CD=14cm,△ABC的周长是:15+13+14=42cm;
当D在线段BC的延长线上时,如图(2):BC=CD-BD=4cm,△ABC的周长是:15+13+4=32cm;
故△ABC的周长是42或32cm.
故答案为:42或32.
 解:直角△ACD中:CD=
解:直角△ACD中:CD=| AC2-AD2 |
| 152-122 |
在直角△ABD中:BD=
| AB2-AD2 |
| 132-122 |
当D在线段BC上时,如图(1):BC=BD+CD=14cm,△ABC的周长是:15+13+14=42cm;
当D在线段BC的延长线上时,如图(2):BC=CD-BD=4cm,△ABC的周长是:15+13+4=32cm;
故△ABC的周长是42或32cm.
故答案为:42或32.
点评:本题主要考查了勾股定理,注意分两种情况讨论是解决本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
计算-a2•a3的结果是( )
| A、a5 |
| B、-a5 |
| C、-a6 |
| D、a6 |
若正比例函数y=kx的图象经过点( 3,2),则k的值为( )
A、-
| ||
B、
| ||
C、-
| ||
D、
|
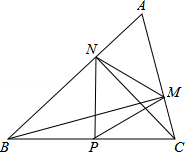 如图,在△ABC中∠A=60°,BM⊥AC于点M,CN⊥AB于点N,P为BC边的中点,连接PM,PN,则下列结论:
如图,在△ABC中∠A=60°,BM⊥AC于点M,CN⊥AB于点N,P为BC边的中点,连接PM,PN,则下列结论: 某图书馆有A、B、C三类图书,它的扇形统计图如图,那么:
某图书馆有A、B、C三类图书,它的扇形统计图如图,那么: