题目内容
17.已知三个数x,y,z满足$\frac{xy}{x+y}$=-3,$\frac{yz}{y+z}$=$\frac{4}{3}$,$\frac{zx}{z+x}=-\frac{4}{3}$,求$\frac{xyz}{xy+yz+zx}$的值.分析 根据反比例函数,可得$\frac{x+y}{xy}=-\frac{1}{3}$,$\frac{y+z}{yz}=\frac{3}{4}$,$\frac{z+x}{z+x}=-\frac{3}{4}$,根据分式的加减,可得答案.
解答 解:∵$\frac{xy}{x+y}$=-3,$\frac{yz}{y+z}$=$\frac{4}{3}$,$\frac{zx}{z+x}=-\frac{4}{3}$,
∴$\frac{x+y}{xy}=-\frac{1}{3}$,$\frac{y+z}{yz}=\frac{3}{4}$,$\frac{z+x}{zx}=-\frac{3}{4}$,
即$\frac{1}{x}$+$\frac{1}{y}$=-$\frac{1}{3}$,$\frac{1}{y}$+$\frac{1}{z}$=$\frac{3}{4}$,$\frac{1}{z}$+$\frac{1}{x}$=-$\frac{3}{4}$,
解得$\frac{1}{x}+\frac{1}{y}+\frac{1}{z}=-\frac{1}{6}$,
$\frac{xz+yz+xy}{xyz}$=-$\frac{1}{6}$,
∴$\frac{xyz}{xy+yz+zx}=\frac{1}{{\frac{1}{z}+\frac{1}{x}+\frac{1}{y}}}=-6$
点评 本题考查了分式的加减,利用比例函数得出$\frac{x+y}{xy}=-\frac{1}{3}$,$\frac{y+z}{yz}=\frac{3}{4}$,$\frac{z+x}{z+x}=-\frac{3}{4}$是解题关键.

练习册系列答案
相关题目
7.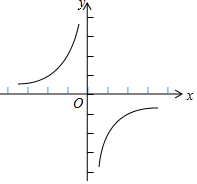 如图,图象对应的函数表达式为( )
如图,图象对应的函数表达式为( )
 如图,图象对应的函数表达式为( )
如图,图象对应的函数表达式为( )| A. | y=5x | B. | $y=\frac{2}{x}$ | C. | $y=\frac{1}{x}$ | D. | $y=-\frac{2}{x}$ |
8.△ABC中,直线DE交AB于点D,交AC于点E,以下能推出DE∥BC的条件是( )
| A. | $\frac{AD}{AB}$=$\frac{3}{4}$,$\frac{AE}{EC}$=$\frac{3}{4}$ | B. | $\frac{AD}{AB}$=$\frac{3}{4}$,$\frac{DE}{BC}$=$\frac{3}{4}$ | C. | $\frac{AD}{DB}$=$\frac{2}{3}$,$\frac{CE}{EA}$=$\frac{2}{3}$ | D. | $\frac{AB}{AD}$=$\frac{4}{3}$,$\frac{EC}{AE}$=$\frac{1}{3}$ |
5.下列运算中能用平方差公式的是( )
| A. | (3x+9)(9x+3) | B. | (2n+5)(n-3) | C. | (2-x)(2+x) | D. | (2+x)(2+x) |
2.下列各式中计算正确的是( )
| A. | x5+x4=x9 | B. | x2•x3=x5 | C. | x3+x3=x6 | D. | (-x2)3=-x5 |
9.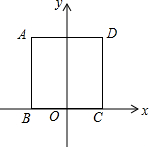 正方形ABCD在直角坐标系中如图放置,B点的坐标是(-2,0),C点的坐标是(2,0),则A点的坐标是( )
正方形ABCD在直角坐标系中如图放置,B点的坐标是(-2,0),C点的坐标是(2,0),则A点的坐标是( )
 正方形ABCD在直角坐标系中如图放置,B点的坐标是(-2,0),C点的坐标是(2,0),则A点的坐标是( )
正方形ABCD在直角坐标系中如图放置,B点的坐标是(-2,0),C点的坐标是(2,0),则A点的坐标是( )| A. | (4,-2) | B. | (-2,1) | C. | (2,4) | D. | (-2,4) |