Question

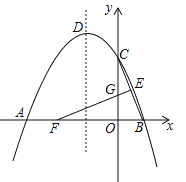
【题目】如图，矩形OABC的顶点A、C分别在x轴和y轴上，点B的坐标为．双曲线的图象经过BC的中点D，且与AB交于点E，连接DE．

（1）求k的值及点E的坐标；

（2）若点F是OC边上一点，且△FBC∽△DEB，求直线FB的解析式．

Answer 1

【答案】（1）k=3，点E的坐标为；（2）

【解析】

（1）首先根据点B的坐标和点D为BC的中点表示出点D的坐标，代入反比例函数的解析式求得k值，然后将点E的横坐标代入求得E点的纵坐标即可；

（2）根据△FBC∽△DEB，利用相似三角形对应边的比相等确定点F的坐标后即可求得直线FB的解析式．

解：（1）∵BC∥x轴，点B的坐标为（2，3），

∴BC=2，

∵点D为BC的中点，

∴CD=1，

∴点D的坐标为（1，3），

代入双曲线y=（x＞0）得；

∵BA∥y轴，

∴点E的横坐标与点B的横坐标相等，为2，

∵点E在双曲线上，

∴y=

∴点E的坐标为（2，）；

（2）∵点E的坐标为（2，），B的坐标为（2，3），点D的坐标为（1，3），

∴BD=1，BE=，BC=2，

∵△FBC∽△DEB，

∴，

即：，

∴FC=，

∴点F的坐标为（0，），

设直线FB的解析式y=kx+b（k≠0），

则，

解得：k=，b=，

∴直线FB的解析式．