题目内容
已知: 反比例函数
经过点B(1,1) ．（1）求该反比例函数解析式；
（2）联结OB，再把点A(2,0)与点B联结,将△OAB绕点O按顺时针方向旋转135°得到△O
，写出的中点P的坐标，试判断点P是否在此双曲线上，并说明理由；（3）若该反比例函数图象上有一点F(m，
)（其中m＞0），在线段OF上任取一点E,设E点的纵坐标为n,过F点作FM⊥x轴于点M，联结EM，使△OEM的面积是
，求代数式
的值．
⑴反比例函数解析式：
………………………………1’
⑵∵已知B(1,1),A(2,0) ∴△OAB是等腰直角三角形
∵顺时针方向旋转135°，
∴B’(0,-
), A’(-,-)
∴中点P为(-, -)．………………………………………2’
∵（-）·（ -）="1 " ………………………………………3’
∴点P在此双曲线上． ……………………………………………4’
⑶∵EH="n" , 0M=m
∴S△OEM=
=
=，∴m=
………………5’
又∵F(m，) 在函数图象上
∴
=1．………………………………………………6’
将m =代入上式，得
-=1
∴
+
=
∴+-2=
……………………7’解析:
略
………………………………1’⑵∵已知B(1,1),A(2,0) ∴△OAB是等腰直角三角形
∵顺时针方向旋转135°，
∴B’(0,-
), A’(-,-) ∴中点P为(-
, -)．………………………………………2’∵（-
）·（ -）="1 " ………………………………………3’ ∴点P在此双曲线上． ……………………………………………4’
⑶∵EH="n" , 0M=m
∴S△OEM=
==，∴m= ………………5’又∵F(m，
) 在函数图象上 ∴
=1．………………………………………………6’将m =
代入上式，得-=1∴
+= ∴+-2=……………………7’解析:略
练习册系列答案
相关题目
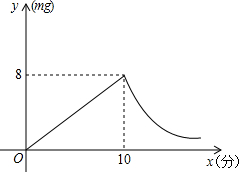烧后，y与x成反比例（如图所示）．现测得药物10分钟燃烧完，此时教室内每立方米空气含药量为8 mg．根据以上信息，解答下列问题：
反比例（如图所示）．现测得药物8分钟燃毕，此时办公室内每立方米空气中含药量为6毫克，据以上信息：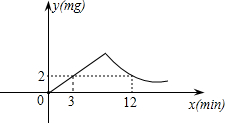
得点燃药物后3min与12min，室内每立方米空气中的含药量为2mg．据以上信息解答下列问题：
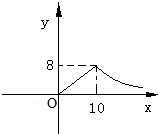信息解答下列问题：
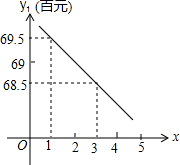（2013•邵东县模拟）重庆市某房地产开发公司在2012年2月以来销售商品房时，市场营销部经分析发现：随着国家政策调控措施的持续影响，大多市民持币观望态度浓厚，从2月起第1周到第五周，房价y1（百元/m2）与周数x（1≤x≤5，且x取正整数）之间存在如图所示的变化趋势：3月中旬由于房屋刚性需求的释放，出现房地产市场“小阳春”行情，房价逆市上扬，从第6周到第12周，房价y2与周数x（6≤x≤12，且x取整数）之间关系如下表：