题目内容
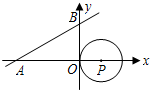 如图,直线y=
如图,直线y=
| ||
| 3 |
| 3 |
| A、2 | B、3 | C、4 | D、5 |
分析:根据直线与坐标轴的交点,得出A,B的坐标,再利用三角形相似得出圆与直线相切时的坐标,进而得出相交时的坐标.
解答: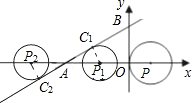 解:∵直线y=
解:∵直线y=
x+
与x轴、y轴分别相交于A,B两点,
圆心P的坐标为(1,0),
∴A点的坐标为:0=
x+
,
x=-3,A(-3,0),
B点的坐标为:(0,
),
∴AB=2
,
将圆P沿x轴向左移动,当圆P与该直线相切于C1时,P1C1=1,
根据△AP1C1∽△ABO,
∴
=
=
,
∴AP1=2,
∴P1的坐标为:(-1,0),
将圆P沿x轴向左移动,当圆P与该直线相切于C2时,P2C2=1,
根据△AP2C2∽△ABO,
∴
=
=
,
∴AP2=2,
P2的坐标为:(-5,0),
从-1到-5,整数点有-2,-3,-4,故横坐标为整数的点P的个数是3个.
故选B.
 解:∵直线y=
解:∵直线y=
| ||
| 3 |
| 3 |
圆心P的坐标为(1,0),
∴A点的坐标为:0=
| ||
| 3 |
| 3 |
x=-3,A(-3,0),
B点的坐标为:(0,
| 3 |
∴AB=2
| 3 |
将圆P沿x轴向左移动,当圆P与该直线相切于C1时,P1C1=1,
根据△AP1C1∽△ABO,
∴
| 1 | ||
|
| AP 1 |
| AB |
| AP1 | ||
2
|
∴AP1=2,
∴P1的坐标为:(-1,0),
将圆P沿x轴向左移动,当圆P与该直线相切于C2时,P2C2=1,
根据△AP2C2∽△ABO,
∴
| 1 | ||
|
| AP2 |
| AB |
| AP 2 | ||
2
|
∴AP2=2,
P2的坐标为:(-5,0),
从-1到-5,整数点有-2,-3,-4,故横坐标为整数的点P的个数是3个.
故选B.
点评:此题主要考查了直线与圆的位置关系,以及相似三角形的判定,题目综合性较强,注意特殊点的求法是解决问题的关键.

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目
 正△ABC.
正△ABC.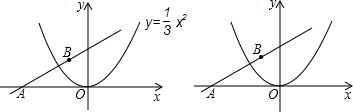
 如图,直线y=-
如图,直线y=- (2012•黄埔区一模)如图,直线
(2012•黄埔区一模)如图,直线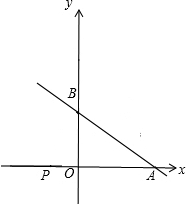 B沿直线AB翻折得到△CAB,点C恰好为经过点A的抛物线的顶点.
B沿直线AB翻折得到△CAB,点C恰好为经过点A的抛物线的顶点.