Question

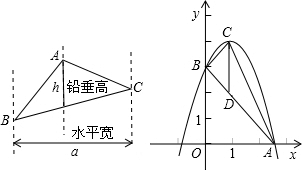
如图：抛物线顶点坐标为点C(1,4),交x轴于点A(3,0)，交y轴于点B.
(1)求抛物线和直线AB的解析式；
(2)点Q（x，0）是x轴上的一动点，过Q点作x轴的垂线，交抛物线于P点、交直线BA于D点，连结OD，PB，当点Q（x，0）在x轴上运动时，求ＰD与x之间的函数关系式；四边形OBPD能否成为平行四边形，若能求出Q点坐标，若不能，请说明理由。
(3) 是否存在一点Q，使以PD为直径的圆与y轴相切，若存在，求出Q点的坐标；若不存在，请说明理由.
        

Answer 1

解：(1)设抛物线的解析式为：
把A（3,0）代入解析式求得
所以································································ 1分
设直线AB的解析式为：
由求得B点的坐标为 
把，代入中
解得：
所以··························································································· 2分
(2设存在符合条件的点Q（x，0），则P点、D点的横坐标都为x，

当PD=OB=3时，四边形OBPD成为平行四边形
，此方程无解，所以不存在点Q。
四边形OBPD不能成为平行四边形······································································· 4分
(3)假设存在一点Q，使以PD为直径的圆与y轴相切
①当时，设半径r


．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．５分           
②当时，设半径为r


．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．６分
③当时，设半径为r


．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．７分所以
、、时都与ｙ轴相切．．．．．．．．９分解析:
略