题目内容
14. 如图,过正方形ABCD的顶点D作DE∥AC交BC的延长线于点E,若BD=8cm,求线段BE的长.
如图,过正方形ABCD的顶点D作DE∥AC交BC的延长线于点E,若BD=8cm,求线段BE的长.
分析 根据正方形的对边互相平行可得AD∥BC,即为AD∥CE,然后根据两组对边互相平行的四边形得出四边形ACED平行四边形;进一步可得BC=AD=CE,再根据正方形的边长等于对角线的$\frac{\sqrt{2}}{2}$倍求出BC,然后求出BE即可.
解答 解:四边形ACED是平行四边形.
理由如下:∵四边形ABCD是正方形,
∴AD∥BC,
即AD∥CE,
∵DE∥AC,
∴四边形ACED是平行四边形;
∴BC=AD=CE=CD,
∵BD=8cm,
∴BC=$\frac{\sqrt{2}}{2}$BD=$\frac{\sqrt{2}}{2}$×8=4$\sqrt{2}$cm,
∴BE=BC+CE=4$\sqrt{2}$+4$\sqrt{2}$=8$\sqrt{2}$cm.
点评 本题考查了正方形的性质,平行四边形的判定与性质,比较简单,熟练掌握各图形的性质是解题的关键.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
4.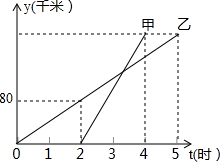 甲、乙两车沿相同路线以各自的速度从A地去往B地,如图表示其行驶过程中路程y(千米)随时间t(小时)的变化图象,下列说法:
甲、乙两车沿相同路线以各自的速度从A地去往B地,如图表示其行驶过程中路程y(千米)随时间t(小时)的变化图象,下列说法:
①乙车比甲车先出发2小时;
②乙车速度为40千米/时;
③A、B两地相距200千米;
④甲车出发80分钟追上乙车.
其中正确的个数为( )
 甲、乙两车沿相同路线以各自的速度从A地去往B地,如图表示其行驶过程中路程y(千米)随时间t(小时)的变化图象,下列说法:
甲、乙两车沿相同路线以各自的速度从A地去往B地,如图表示其行驶过程中路程y(千米)随时间t(小时)的变化图象,下列说法:①乙车比甲车先出发2小时;
②乙车速度为40千米/时;
③A、B两地相距200千米;
④甲车出发80分钟追上乙车.
其中正确的个数为( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
5.计算:$\root{3}{0.064}$+$\sqrt{1-\frac{9}{25}}$-$\sqrt{1{7}^{2}-{8}^{2}}$÷$\root{3}{-\frac{1}{125}}$.
19.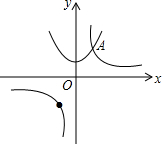 如图,抛物线y=x2+1与双曲线y=$\frac{k}{x}$的交点A的横坐标是1,则关于x的不等式$\frac{k}{x}<{x^2}$+1的解集是( )
如图,抛物线y=x2+1与双曲线y=$\frac{k}{x}$的交点A的横坐标是1,则关于x的不等式$\frac{k}{x}<{x^2}$+1的解集是( )
 如图,抛物线y=x2+1与双曲线y=$\frac{k}{x}$的交点A的横坐标是1,则关于x的不等式$\frac{k}{x}<{x^2}$+1的解集是( )
如图,抛物线y=x2+1与双曲线y=$\frac{k}{x}$的交点A的横坐标是1,则关于x的不等式$\frac{k}{x}<{x^2}$+1的解集是( )| A. | x>1 | B. | x<0 | C. | 0<x<1 | D. | x<0或x>1 |
4.2014年我省通过实施土地整治项目,累计新增耕地30.07万亩,30.07万用科学记数法表示正确的是( )
| A. | 30.07×104 | B. | 3.007×105 | C. | 300.7×103 | D. | 0.3007×106 |
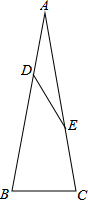 在△ABC中,AB=AC,点D在AB上,点E在AC上,且AD=DE=EC=BC.求证:∠BAC=20°.
在△ABC中,AB=AC,点D在AB上,点E在AC上,且AD=DE=EC=BC.求证:∠BAC=20°.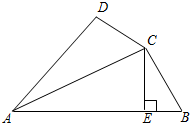 如图,在四边形ABCD中,AC平分∠BAD,CE⊥AB于点E.
如图,在四边形ABCD中,AC平分∠BAD,CE⊥AB于点E.