题目内容
如图,△ABC是等边三角形,点D是线段AC上的一动点,E在BC的延长线上,且BD=DE.
(1)如图1,若点D为线段AC的中点,求证:AD=CE;
(2)如图2,若点D为线段AC上任意一点,试确定线段AD与CE的大小关系,并说明理由.
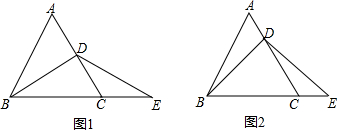
(1)如图1,若点D为线段AC的中点,求证:AD=CE;
(2)如图2,若点D为线段AC上任意一点,试确定线段AD与CE的大小关系,并说明理由.

考点:全等三角形的判定与性质,等边三角形的性质
专题:
分析:(1)根据等边三角形三线合一的性质即可求得∠DBC的度数,根据BD=DE即可解题;
(2)作DF∥AB,可证△≌BDF△EDC,可得BF=CE,再证AD=BF即可解题.
(2)作DF∥AB,可证△≌BDF△EDC,可得BF=CE,再证AD=BF即可解题.
解答:解:(1)∵点D为线段AC的中点,
∴BD平分∠ABC,
∴∠DBE=30°,
∵BD=DE,
∴∠E=∠DBE=30°,
∵∠DCE=180°-∠ACB=120°,
∴∠CDE=180°-120°-30°=30°,
∴AD=CE;
(2)作DF∥AB,
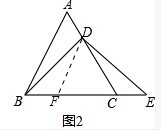
∵DF∥AB,
∴
=
,
∴BF=AD,
∵DF∥AB,
∴∠DFC=60°,
∴∠BFD=120°,
∵BD=DE,
∴∠E=∠DBE,
在△BDF和△EDC中,
,
∴△BDF≌△EDC,(AAS)
∴BF=CE,
∴AD=CE.
∴BD平分∠ABC,
∴∠DBE=30°,
∵BD=DE,
∴∠E=∠DBE=30°,
∵∠DCE=180°-∠ACB=120°,
∴∠CDE=180°-120°-30°=30°,
∴AD=CE;
(2)作DF∥AB,

∵DF∥AB,
∴
| CF |
| BF |
| CD |
| AD |
∴BF=AD,
∵DF∥AB,
∴∠DFC=60°,
∴∠BFD=120°,
∵BD=DE,
∴∠E=∠DBE,
在△BDF和△EDC中,
|
∴△BDF≌△EDC,(AAS)
∴BF=CE,
∴AD=CE.
点评:本题考查了全等三角形的判定,考查了全等三角形对应边相等的性质,本题中求证△BDF≌△EDC是解题的关键.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案
相关题目
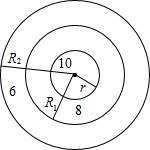 一只靶子的环数如图,假设子弹击中靶子中的每一点是等可能的.已知靶中心10环的半径r=10cm,8环的半径R1=20cm,6环的半径R2=40cm.
一只靶子的环数如图,假设子弹击中靶子中的每一点是等可能的.已知靶中心10环的半径r=10cm,8环的半径R1=20cm,6环的半径R2=40cm. 如图,在Rt△ABC中,AB=9,BC=6,∠B=90°,将△ABC折叠,使A点与BC的中点D重合,折痕为MN,求线段BN的长.
如图,在Rt△ABC中,AB=9,BC=6,∠B=90°,将△ABC折叠,使A点与BC的中点D重合,折痕为MN,求线段BN的长. PA,PB切⊙O于点A、B,CD切⊙O于点E.
PA,PB切⊙O于点A、B,CD切⊙O于点E.