题目内容
已知关于x的方程kx2-2(k+1)x+k-1=0有两个不相等的实数根.
(1)求k的取值范围;
(2)是否存在实数k,使此方程的两个实数根的倒数和等于0?若存在,求出k的值;若不存在,说明理由.
解:(1)∵方程有两个不相等的实数根,
∴△=[-2(k+1)]2-4k(k-1)=12k+4>0,且k≠0
解得k>- ,且k≠0,
,且k≠0,
即k的取值范围是k>- ,且k≠0;
,且k≠0;
(2)假设存在实数k,使得方程的两个实数根x1,x2的倒数和为0,
则x1,x2不为0,且 ,
,
即 ,且
,且 ,
,
解得k=-1,
而k=-1与方程有两个不相等实根的条件k>-1,且k≠0矛盾,
故使方程的两个实数根的倒数和为0的实数k不存在

练习册系列答案
 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案
相关题目
 的值为0,则
的值为0,则 = .
= . (
(
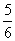 B.1 C.
B.1 C.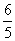 D.2
D.2 

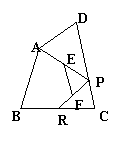 C.线段EF的长不变
C.线段EF的长不变  D.线段EF的长与点P的位置有关
D.线段EF的长与点P的位置有关
 =_________.
=_________.