题目内容
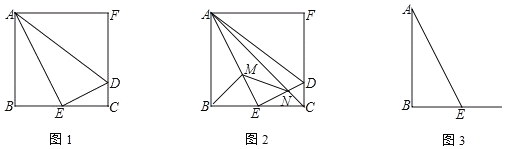
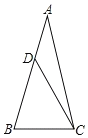
【题目】如图,△ABC中,AB=AC,∠A=30°,点D在边AB上,∠ACD=15°,则![]() ____.
____.
【答案】![]() .
.
【解析】
根据题意作CE⊥AB于E,作DF⊥AC于F,在CF上截取一点H,使得CH=DH,连接DH,并设AD=2x,解直角三角形求出BC(用x表示)即可解决问题.
解:作CE⊥AB于E,作DF⊥AC于F,在CF上截取一点H,使得CH=DH,连接DH.
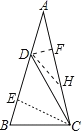
设AD=2x,
∵AB=AC,∠A=30°,
∴∠ABC=∠ACB=75°,DF![]() AD=x,AF
AD=x,AF![]() x,
x,
∵∠ACD=15°,HD=HC,
∴∠HDC=∠HCD=15°,
∴∠FHD=∠HDC+∠HCD=30°,
∴DH=HC=2x,FH![]() x,
x,
∴AB=AC=2x+2![]() x,
x,
在Rt△ACE中,EC![]() AC=x
AC=x![]() x,AE
x,AE![]() EC
EC![]() x+3x,
x+3x,
∴BE=AB﹣AE![]() x﹣x,
x﹣x,
在Rt△BCE中,BC![]() 2
2![]() x,
x,
∴![]() .
.
故答案为:![]() .
.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目