题目内容
已知a2+
=2,则
= .
| 1 |
| a2 |
| a2-a+1 |
| a2+1 |
考点:分式的化简求值
专题:
分析:先根据a2+
=2求出a+
的值,再把原式进行化简,把a+
的值代入进行计算即可.
| 1 |
| a2 |
| 1 |
| a |
| 1 |
| a |
解答:解:∵a2+
=2,
∴(a+
)2=4,
∴a+
=2或a+
=-2.
∵
有意义,
∴a≠0,
∴原式=
,
当a+
=2时,原式=
=
;
当a+
=-2时,原式=
=
.
故答案为:
或
.
| 1 |
| a2 |
∴(a+
| 1 |
| a |
∴a+
| 1 |
| a |
| 1 |
| a |
∵
| 1 |
| a2 |
∴a≠0,
∴原式=
a+
| ||
a+
|
当a+
| 1 |
| a |
| 2-1 |
| 2 |
| 1 |
| 2 |
当a+
| 1 |
| a |
| -2-1 |
| -2 |
| 3 |
| 2 |
故答案为:
| 1 |
| 2 |
| 3 |
| 2 |
点评:本题考查的是分式的化简求值,熟知分式混合运算的法则是解答此题的关键.

练习册系列答案
相关题目
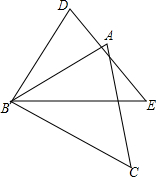 如图,AB=DB,∠CBE=∠ABD,请添加一个条件使△ABC≌△DBE,则需添加的条件是
如图,AB=DB,∠CBE=∠ABD,请添加一个条件使△ABC≌△DBE,则需添加的条件是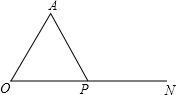 如图,已知AO=10,P是射线ON上一动点(即P点可在射线ON上运动),∠AON=60°.
如图,已知AO=10,P是射线ON上一动点(即P点可在射线ON上运动),∠AON=60°.