题目内容
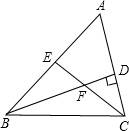 已知:如图,△ABC中,∠A=70°,∠ABC=48°,BD⊥AC于D,CE是∠ACB的平分线,BD与CE交于点F,求∠CBD、∠EFD的度数.
已知:如图,△ABC中,∠A=70°,∠ABC=48°,BD⊥AC于D,CE是∠ACB的平分线,BD与CE交于点F,求∠CBD、∠EFD的度数.
分析:根据三角形的内角和定理得到∠ACB=180°-∠A-∠ABC=180°-70°-48°=62°,利用角平分线的定义得到∠ACE,再根据互余求出∠CBD=90°-∠ACB;根据三角形外角的性质得到∠EFD=∠ACE+∠BDC.
解答:解:∵∠A+∠ABC+∠ACB=180°,
∴∠ACB=180°-∠A-∠ABC=180°-70°-48°=62°.
∵BD⊥AC,
∴∠BDC=90°.
∴∠CBD=90°-∠ACB=90°-62°=28°;
∵CE是∠ACB的平分线,
∴∠ACE=
∠ACB=
×62°=31°.
∴∠EFD=∠ACE+∠BDC=31°+90°=121°.
故答案为:∠CBD、∠EFD的度数分别为28°,121°.
∴∠ACB=180°-∠A-∠ABC=180°-70°-48°=62°.
∵BD⊥AC,
∴∠BDC=90°.
∴∠CBD=90°-∠ACB=90°-62°=28°;
∵CE是∠ACB的平分线,
∴∠ACE=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠EFD=∠ACE+∠BDC=31°+90°=121°.
故答案为:∠CBD、∠EFD的度数分别为28°,121°.
点评:本题考查了三角形的内角和定理:三角形的内角和为180°.也考查了三角形外角的性质以及角平分线的性质.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 17、已知,如图,△ABC中,∠BAC=90°,AD⊥BC于点D,BE平分∠ABC,交AD于点M,AN平分∠DAC,交BC于点N.
17、已知,如图,△ABC中,∠BAC=90°,AD⊥BC于点D,BE平分∠ABC,交AD于点M,AN平分∠DAC,交BC于点N. 已知:如图,∠ABC、∠ACB 的平分线相交于点F,过F作DE∥BC于D,交AC 于E,且AB=6,AC=5,求三角形ADE的周长.
已知:如图,∠ABC、∠ACB 的平分线相交于点F,过F作DE∥BC于D,交AC 于E,且AB=6,AC=5,求三角形ADE的周长. 已知:如图,△ABC是等边三角形,点D在AB上,点E在AC的延长线上,且BD=CE,DE交BC于F,求证:BF=CF+CE.
已知:如图,△ABC是等边三角形,点D在AB上,点E在AC的延长线上,且BD=CE,DE交BC于F,求证:BF=CF+CE. 已知:如图,△ABC中,AB=AC=10,BC=16,点D在BC上,DA⊥CA于A.
已知:如图,△ABC中,AB=AC=10,BC=16,点D在BC上,DA⊥CA于A. 已知:如图,△ABC中,AD⊥BC,BD=DE,点E在AC的垂直平分线上.
已知:如图,△ABC中,AD⊥BC,BD=DE,点E在AC的垂直平分线上.