题目内容
 24、如图,已知DM平分∠ADC,BM平分∠ABC,且∠A=27°,∠M=33°,求∠C的度数.
24、如图,已知DM平分∠ADC,BM平分∠ABC,且∠A=27°,∠M=33°,求∠C的度数.分析:设BC与MD的交点为E,由DM平分∠ADC,BM平分∠ABC,得∠CDQ=2∠1,∠ABQ=2∠2,利用三角形的内角和定理可得,∠C+2∠1=∠A+2∠2①,∠C+∠1=∠M+∠2②,则∠C=2∠M-∠A,而∠A=27°,∠M=33°,即可求出∠C.
解答: 解:设BC与MD的交点为E,如图,
解:设BC与MD的交点为E,如图,
∵DM平分∠ADC,BM平分∠ABC,
∴∠CDQ=2∠1,∠ABQ=2∠2,
在△CDQ和△ABQ中,∠CQD=∠AQB,
∴∠C+2∠1=∠A+2∠2,①
在△CDE和△MBE中,∠CED=∠MEB,
∴∠C+∠1=∠M+∠2,②
用②×2-①得,∠C=2∠M-∠A,
而∠A=27°,∠M=33°,
∴∠C=2×33°-27°=39°.
故答案为:39°.
 解:设BC与MD的交点为E,如图,
解:设BC与MD的交点为E,如图,∵DM平分∠ADC,BM平分∠ABC,
∴∠CDQ=2∠1,∠ABQ=2∠2,
在△CDQ和△ABQ中,∠CQD=∠AQB,
∴∠C+2∠1=∠A+2∠2,①
在△CDE和△MBE中,∠CED=∠MEB,
∴∠C+∠1=∠M+∠2,②
用②×2-①得,∠C=2∠M-∠A,
而∠A=27°,∠M=33°,
∴∠C=2×33°-27°=39°.
故答案为:39°.
点评:本题考查了三角形的内角和定理:三角形的内角和为180°.也考查了角平分线的性质.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
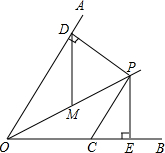 (2013•西宁)如图,已知OP平分∠AOB,∠AOB=60°,CP=2,CP∥OA,PD⊥OA于点D,PE⊥OB于点E.如果点M是OP的中点,则DM的长是( )
(2013•西宁)如图,已知OP平分∠AOB,∠AOB=60°,CP=2,CP∥OA,PD⊥OA于点D,PE⊥OB于点E.如果点M是OP的中点,则DM的长是( ) 如图,已知DM平分∠ADC,BM平分∠ABC,∠A=36°,∠M=44°,求∠C的度数.
如图,已知DM平分∠ADC,BM平分∠ABC,∠A=36°,∠M=44°,求∠C的度数. ,CP
,CP ,CP∥OA,PD⊥OA于点D,PE⊥OB于点E.如果点M是OP的中点,则DM的长是
,CP∥OA,PD⊥OA于点D,PE⊥OB于点E.如果点M是OP的中点,则DM的长是
 B.
B. C.
C. D.
D.
 如图,已知DM平分∠ADC,BM平分∠ABC,∠A=36°,∠M=44°,求∠C的度数.
如图,已知DM平分∠ADC,BM平分∠ABC,∠A=36°,∠M=44°,求∠C的度数.