题目内容
已知:BD、CE是△ABC的两条高,

(1)求证△ADE∽△ABC
(2)若∠A=60°,求(1)中的相似比
(2)若∠A=60°,求(1)中的相似比
(1)证明:∵BD、CE是△ABC的两条高
∴∠ADB=∠AEC=90°
∵∠A=∠A
∴△ADB∽△AEC
∴AD:AE=AB:AC 即AD:AB=AE:AC
∵∠A=∠A ∴△ADE∽△ABC;
(2)在Rt△ADB中, ∠ADB=90°, ∠A=60°
∴∠ABD=90°- 60°=30°
∴AD=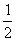 AB 即
AB 即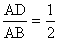
∴∠ADB=∠AEC=90°
∵∠A=∠A
∴△ADB∽△AEC
∴AD:AE=AB:AC 即AD:AB=AE:AC
∵∠A=∠A ∴△ADE∽△ABC;
(2)在Rt△ADB中, ∠ADB=90°, ∠A=60°
∴∠ABD=90°- 60°=30°
∴AD=
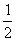 AB 即
AB 即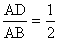

练习册系列答案
相关题目