题目内容
 如图,D为△ABC的边AC上的一点,∠DBC=∠A,已知BC=
如图,D为△ABC的边AC上的一点,∠DBC=∠A,已知BC=| 2 |
分析:根据已知条件,先证明△BCD∽△ACB,再根据相似三角形的面积比是相似比的平方来求CD的长度.
解答:解:在△BCD和△ABC中,
∠DBC=∠A(已知),∠C=∠C(公共角),
∴△BCD∽△ABC,
∴(
)2=
,
解得,CD=±
,
∵CD>0,
∴CD=-
(舍去),
∴CD=
.
∠DBC=∠A(已知),∠C=∠C(公共角),
∴△BCD∽△ABC,
∴(
| CD |
| BC |
| 2 |
| 3 |
解得,CD=±
| 2 |
| 3 |
| 3 |
∵CD>0,
∴CD=-
| 2 |
| 3 |
| 3 |
∴CD=
| 2 |
| 3 |
| 3 |
点评:解答本题的关键是熟练掌握“相似三角形的面积比是相似比的平方”这一知识点.

练习册系列答案
相关题目
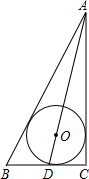 如图,⊙O为△ABC的内切圆,∠C=90度,OA的延长线交BC于点D,AC=4,CD=1,则⊙O的半径等于( )
如图,⊙O为△ABC的内切圆,∠C=90度,OA的延长线交BC于点D,AC=4,CD=1,则⊙O的半径等于( )A、
| ||
B、
| ||
C、
| ||
D、
|
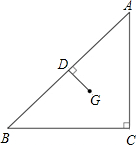 如图,G为△ABC的重心,其中∠C=90°,D在AB上,GD⊥AB.若AB=29,AC=20,BC=21,则GD的长度为何?( )
如图,G为△ABC的重心,其中∠C=90°,D在AB上,GD⊥AB.若AB=29,AC=20,BC=21,则GD的长度为何?( )| A、7 | ||
B、14
| ||
C、
| ||
D、
|
 6、如图,⊙O为△ABC的外接圆,BC为直径,AC=AB,则∠D的度数为( )
6、如图,⊙O为△ABC的外接圆,BC为直径,AC=AB,则∠D的度数为( ) 25、如图,AD为△ABC的高,E为AC上一点,BE交AD于F,且有BF=AC,FD=CD,那么BE⊥AC吗?为什么?
25、如图,AD为△ABC的高,E为AC上一点,BE交AD于F,且有BF=AC,FD=CD,那么BE⊥AC吗?为什么?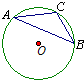 5、如图,⊙O为△ABC的外接圆,且∠A=30°,AB=8cm,BC=5cm,则⊙O的半径=
5、如图,⊙O为△ABC的外接圆,且∠A=30°,AB=8cm,BC=5cm,则⊙O的半径=