Question

【题目】已知矩形ABCD中，，，现有两只蚂蚁P和Q同时分别从A、B出发，沿方向前进，蚂蚁P每秒走1cm，蚂蚁Q每秒走2cm．问：

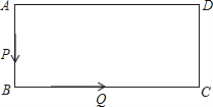
（1）蚂蚁出发后△PBQ第一次是等腰三角形需要爬行几秒?

（2）P、Q两只蚂蚁最快爬行几秒后，直线PQ与边AB平行?

Answer 1

【答案】（1）蚂蚁出发后△PBQ第一次是等腰三角形需要爬行秒；（2）P、Q两只蚂蚁最快爬行20秒后,直线PQ∥AB

【解析】

（1）首先设蚂蚁出发后△PBQ第一次是等腰三角形需要爬行t秒，可得方程：10-t=2t，解此方程即可求得答案；

（2）首先设P、Q两只蚂蚁最快爬行x秒后，直线PQ∥AB，可得方程：x-10=50-2x，解此方程即可求得答案.

(1)设蚂蚁出发后△PBQ第一次是等腰三角形需要爬行t秒，

∵四边形ABCD是长方形，

∴∠B=90，

∴BP=BQ，

∵AP=tcm,BQ=2tcm,则PB=ABAP=10t(cm)，

∴10t=2t，

解得：t=，

∴蚂蚁出发后△PBQ第一次是等腰三角形需要爬行秒；

(2)设P、Q两只蚂蚁最快爬行x秒后,直线PQ∥AB，

∵AD∥BC，

∴四边形ABPQ是平行四边形，

∴AQ=BP，

∴x10=502x，

解得：x=20，

∴P、Q两只蚂蚁最快爬行20秒后,直线PQ∥AB；