��Ŀ����
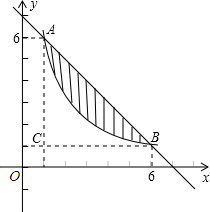 ��ͼ����ƽ��ֱ������ϵ�У��е�A��1��6������B ��6��1������C��1��1�����㣮
��ͼ����ƽ��ֱ������ϵ�У��е�A��1��6������B ��6��1������C��1��1�����㣮��1������A�ں���y=
| m |
| x |
����m��ֵ��ֱ��AB�Ľ���ʽ��
����������OAB�������
����y���Ƿ����һ��Pʹ��OCPΪ���������Σ������ڣ�ֱ��д����P�����ꣻ�������ڣ���˵�����ɣ�
�����һ����ĺᡢ�������Ϊ��������ô���dz�������Ǹ�㣮��ֱ��д��ͼ����Ӱ���֣��������߽磩�����������꣮
��2��������y=
| m |
| x |
��������1���ٰѵ�A ��1��6�����뺯��y=
��x��0�����m��ֵ����ֱ��AB����ʽΪy=kx+b����A��B�������k��b��ֵ������ȷ����ֱ��AB�Ľ���ʽ��
������OA��OB��������AOB���=������AOD���+����ADEB���-������OBE�����������ɣ�
����ͼ��ʾ��������������ǣ���OP1=P1C=1ʱ����OP1CΪ���������Σ���CP2=OC=
ʱ����OP2CΪ���������Σ���OP3=OC=
ʱ����OP3CΪ���������Σ���OP4=OC=
ʱ����OP4CΪ���������Σ��ֱ������ӦP�����꼴�ɣ�
����ͼ���ҳ���������ĸ�����꼴�ɣ�
��2��ץס�����ؼ��㣬һ�Ƿ���������ͼ���AB�е�ʱ��һ�Ƿ���������ͼ���C��ʱ���ֱ������Ӧm��ֵ������ȷ������������m�ķ�Χ��
| m |
| x |
������OA��OB��������AOB���=������AOD���+����ADEB���-������OBE�����������ɣ�
����ͼ��ʾ��������������ǣ���OP1=P1C=1ʱ����OP1CΪ���������Σ���CP2=OC=
| 2 |
| 2 |
| 2 |
����ͼ���ҳ���������ĸ�����꼴�ɣ�
��2��ץס�����ؼ��㣬һ�Ƿ���������ͼ���AB�е�ʱ��һ�Ƿ���������ͼ���C��ʱ���ֱ������Ӧm��ֵ������ȷ������������m�ķ�Χ��
��� �⣺��1���ٽ�A��1��6�����뷴��������ʽ�ã�6=
�⣺��1���ٽ�A��1��6�����뷴��������ʽ�ã�6=
����m=6��
��ֱ��AB����ʽΪy=kx+b��
��A��1��6����B��6��1������ã�
��
��ã�
��
��ֱ��AB�Ľ���ʽΪy=-x+7��
������OA��OB��������ã�AD=OE=6��OD=BE=1��DE=OE-OD=5��
��S��OAB=S��AOD+S����ADEB-S��BEO
=
��1��6+
��5����1+6��-
��1��6
=
��
����ͼ��ʾ��
��OP1=P1C=1ʱ����OP1CΪ���������Σ���ʱP1��0��1����
��CP2=OC=
ʱ����OP2CΪ���������Σ���ʱP2��0��2����
��OP3=OC=
ʱ����OP3CΪ���������Σ���ʱP3��0��
����
��OP4=OC=
ʱ����OP4CΪ���������Σ���ʱP4��0��-
����
���ϣ�P������Ϊ��0��1����0��2����0��
����0��-
����
�ܸ���ͼ�εã�������꣨2��4������3��3������4��2����
��2����˫���߾�����C��1��1��ʱ��m=1��
��˫���߾���AB�е㣨
��
��ʱ��m=
��
����y=
��x��0����ͼ�����ABC�й�����ʱm��ȡֵ��Χ��1��m��
��
 �⣺��1���ٽ�A��1��6�����뷴��������ʽ�ã�6=
�⣺��1���ٽ�A��1��6�����뷴��������ʽ�ã�6=| m |
| 1 |
��ֱ��AB����ʽΪy=kx+b��
��A��1��6����B��6��1������ã�
|
��ã�
|
��ֱ��AB�Ľ���ʽΪy=-x+7��
������OA��OB��������ã�AD=OE=6��OD=BE=1��DE=OE-OD=5��
��S��OAB=S��AOD+S����ADEB-S��BEO
=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=
| 35 |
| 2 |
����ͼ��ʾ��

��OP1=P1C=1ʱ����OP1CΪ���������Σ���ʱP1��0��1����
��CP2=OC=
| 2 |
��OP3=OC=
| 2 |
| 2 |
��OP4=OC=
| 2 |
| 2 |
���ϣ�P������Ϊ��0��1����0��2����0��
| 2 |
| 2 |
�ܸ���ͼ�εã�������꣨2��4������3��3������4��2����
��2����˫���߾�����C��1��1��ʱ��m=1��
��˫���߾���AB�е㣨
| 7 |
| 2 |
| 7 |
| 2 |
| 49 |
| 4 |
����y=
| m |
| x |
| 49 |
| 4 |
�������������ڷ����������ۺ��⣬�漰��֪ʶ�У�������ͼ�����ʣ����������ε����ʣ�������������ͼ�������ʣ�����ϵ������������ʽ�������˷������ۼ����ν�ϵ�˼�룬��һ���е��⣮

��ϰ��ϵ�д�
 ��У����ϵ�д�
��У����ϵ�д�
�����Ŀ
 ��ͼ����ƽ��ֱ�������У��ı���OABC�ǵ������Σ�CB��OA��OA=7��AB=4����COA=60�㣬��PΪx���ϵ�һ�����㣬���ǵ�P�����0����A�غϣ�����CP��D�����߶�AB��һ�㣬����PD��
��ͼ����ƽ��ֱ�������У��ı���OABC�ǵ������Σ�CB��OA��OA=7��AB=4����COA=60�㣬��PΪx���ϵ�һ�����㣬���ǵ�P�����0����A�غϣ�����CP��D�����߶�AB��һ�㣬����PD�� ��2012•�山��һģ����ͼ����ƽ��ֱ������xoy�У�������ԭ��OΪԲ�ģ�3Ϊ�뾶��Բ���Ӵ�Բ�ڣ������߽磩�����������㣨�ᡢ�������Ϊ������������ѡȡһ���㣬��ᡢ������֮��Ϊ0�ĸ�����
��2012•�山��һģ����ͼ����ƽ��ֱ������xoy�У�������ԭ��OΪԲ�ģ�3Ϊ�뾶��Բ���Ӵ�Բ�ڣ������߽磩�����������㣨�ᡢ�������Ϊ������������ѡȡһ���㣬��ᡢ������֮��Ϊ0�ĸ����� ��ͼ����ƽ��ֱ�������У���������ABCD���µ���x���ϣ���B������Ϊ��4��0����D������Ϊ��0��3������AC��Ϊ
��ͼ����ƽ��ֱ�������У���������ABCD���µ���x���ϣ���B������Ϊ��4��0����D������Ϊ��0��3������AC��Ϊ ��ͼ����ƽ��ֱ������xOy�У���֪��A��-5��0����P�Ƿ���������
��ͼ����ƽ��ֱ������xOy�У���֪��A��-5��0����P�Ƿ��������� ��COA=45�㣬����P�ӵ�O������������OABC�ı����˶���·��ΪO��A��B��C�������Cʱֹͣ����ֱ��CP��
��COA=45�㣬����P�ӵ�O������������OABC�ı����˶���·��ΪO��A��B��C�������Cʱֹͣ����ֱ��CP��