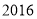题目内容
已知:点C、A、D在同一条直线上,∠ABC=∠ADE=α,线段 BD、CE交于点M.
(1)如图1,若AB=AC,AD=AE
①问线段BD与CE有怎样的数量关系?并说明理由;②求∠BMC的大小(用α表示);
(2)如图2,若AB= BC=kAC,AD =ED=kAE 则线段BD与CE的数量关系为 ,∠BMC= (用α表示);
(3)在(2)的条件下,把△ABC绕点A逆时针旋转180°,在备用图中作出旋转后的图形(要求:尺规作图,不写作法,保留作图痕迹),连接 EC并延长交BD于点M.则∠BMC= (用α表示).
练习册系列答案
相关题目


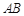 垂直于弦CD,垂足是E, ∠A=22.5°,OC=4, CD的长为 ( )
垂直于弦CD,垂足是E, ∠A=22.5°,OC=4, CD的长为 ( )
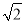 B.
B. 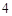 C. 4
C. 4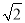 D. 8
D. 8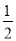 B. 2m2n与2n2m C.
B. 2m2n与2n2m C. 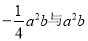 D.
D. 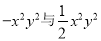
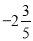 的相反数是__________;绝对值是__________;倒数是__________.
的相反数是__________;绝对值是__________;倒数是__________.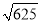 的算术平方根是
的算术平方根是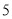 ;②
;②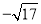 是
是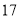 的平方根;③
的平方根;③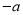 没有平方根;④
没有平方根;④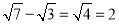 ;⑤
;⑤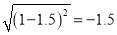 .其中正确的有( ).
.其中正确的有( ).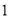 个 B.
个 B. 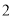 个 C.
个 C. 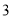 个 D.
个 D. 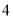 个
个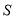 (米)与时间
(米)与时间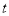 (秒)的函数关系式是_________.
(秒)的函数关系式是_________.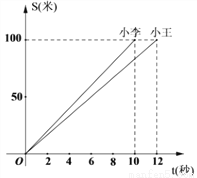
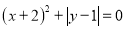 则
则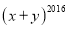 的值为( )
的值为( )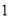 B.
B. 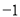 C.
C. 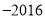 D.
D.