题目内容
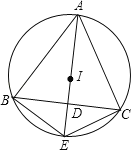
【题目】如图,![]() 是
是![]() 的直径,点
的直径,点![]() 在
在![]() 上,
上,![]() 的平分线交
的平分线交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() .过点
.过点![]() 作
作![]() 的切线
的切线![]() 交
交![]() 的延长线于点
的延长线于点![]() ,连接
,连接![]() ,
,![]() .
.
(1)求证:![]() ,
,![]() ;
;
(2)过点![]() 分别作直线
分别作直线![]() ,
,![]() 垂线,垂足为
垂线,垂足为![]() ,
,![]() .若
.若![]() ,
,![]() ,请你完成示意图并求线段
,请你完成示意图并求线段![]() 的长.
的长.
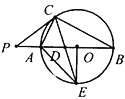
【答案】(1)证明见解析;(2)画图见解析,7
【解析】
(1)图1中,连接![]() ,由AB是直径可得
,由AB是直径可得![]() ,由角平分线的定义可求∠ECA=45°,然后根据圆周角定理可求
,由角平分线的定义可求∠ECA=45°,然后根据圆周角定理可求![]() ;由OC=OE可证
;由OC=OE可证![]() ,然后利用余角的性质证明
,然后利用余角的性质证明![]() 可证
可证![]() ;
;
(2)如图2中.作EH⊥BC于H,EF⊥CA于F.首先证明Rt△AEF≌Rt△BEH,推出AF=BH,设AF=BH=x,再证明四边形CFEH是正方形,推出CF=CH,可得6+x=8-x,推出x=1即可解决问题;
(1)证明:①如图1中,连接![]() ,
,
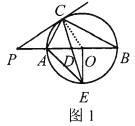
∵![]() 直径,
直径,
∴![]() ,
,
∴![]() 平分
平分![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.
∵![]() 是切线,
是切线,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() .
.
(2)如图2中,连接![]() ,过点
,过点![]() 作
作![]() 于
于![]() ,
,![]() 于
于![]() .
.
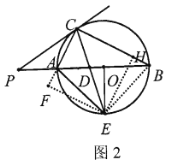
又∵![]() 平分
平分![]() ,
,
∴![]() ,
,![]() ,
,
由(1)得![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,设
,设![]() ,
,
∵![]() ,
,
∴四边形![]() 是矩形,
是矩形,
∵![]() ,
,
∴四边形![]() 是正方形,
是正方形,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.

练习册系列答案
相关题目