题目内容
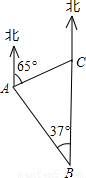
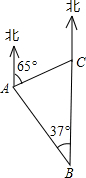 如图,一巡逻艇航行至海面B处时,得知其正北方向上C处一渔船发生故障,已知港口A处在B处的北偏西37°方向上,距B处20海里;C处在A处的北偏东65°方向上.求B,C之间的距离.(结果精确到0.1海里)(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,sin65°≈0.91,cos65°≈0.42,tan65°≈2.14.)
如图,一巡逻艇航行至海面B处时,得知其正北方向上C处一渔船发生故障,已知港口A处在B处的北偏西37°方向上,距B处20海里;C处在A处的北偏东65°方向上.求B,C之间的距离.(结果精确到0.1海里)(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,sin65°≈0.91,cos65°≈0.42,tan65°≈2.14.)
分析:由已知可得△ABC中∠C=65°,∠B=37°且AB=20海里.要求BC的长,可以过A作AD⊥BC于D,先求出CD和BD的长,就可转化为运用三角函数解直角三角形.
解答: 解:过点A作AD⊥BC,垂足为D.
解:过点A作AD⊥BC,垂足为D.
在Rt△ABD中,AB=20,∠B=37°,
∴AD=AB•sin37°=20sin37°≈12,
BD=AB•cos37°=20cos37°≈16.
在Rt△ADC中,∠ACD=65°,
∴CD=
≈
≈5.61.
∴BC=BD+CD≈5.61+16=21.61≈21.6(海里).
答:B、C之间的距离约为21.6海里.
 解:过点A作AD⊥BC,垂足为D.
解:过点A作AD⊥BC,垂足为D.在Rt△ABD中,AB=20,∠B=37°,
∴AD=AB•sin37°=20sin37°≈12,
BD=AB•cos37°=20cos37°≈16.
在Rt△ADC中,∠ACD=65°,
∴CD=
| AD |
| tan65° |
| 12 |
| 2.14 |
∴BC=BD+CD≈5.61+16=21.61≈21.6(海里).
答:B、C之间的距离约为21.6海里.
点评:解一般三角形的问题一般可以转化为解直角三角形的问题,解决的方法就是作高线.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
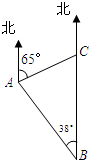 如图,一巡逻艇航行至海面B处时,得知其正北方向上C处一渔船发生故障.已知港口A处在B处的北偏西38°方向上,距B处20海里;C处在A处的北偏东65°方向上.求B,C之间的距离(结果精确到1海里).
如图,一巡逻艇航行至海面B处时,得知其正北方向上C处一渔船发生故障.已知港口A处在B处的北偏西38°方向上,距B处20海里;C处在A处的北偏东65°方向上.求B,C之间的距离(结果精确到1海里).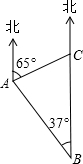 如图,一巡逻艇航行至海面B处时,得知其正北方向上C处一渔船发生故障.已知港口A处在B处的北偏西37°方向上,距B处20海里;C处在A处的北偏东65°方向上.求BC之间的距离(结果精确到0.1海里).
如图,一巡逻艇航行至海面B处时,得知其正北方向上C处一渔船发生故障.已知港口A处在B处的北偏西37°方向上,距B处20海里;C处在A处的北偏东65°方向上.求BC之间的距离(结果精确到0.1海里).