题目内容
△ABC,AB=AC,BC=8,AB长是方程x2-9x+20=0的一个根,求等腰三角形ABC的面积.
 解:解方程x2-9x+20=0得x1=4,x2=5.
解:解方程x2-9x+20=0得x1=4,x2=5.∵AB长是方程x2-9x+20=0的一个根,
∴AB=4或AB=5.
∵AB=AC,BC=8,AB+AC>BC,
∴2AB>8,
∴AB>4,
∴AB=5.
如图,过点A作AD⊥BC于点D.则BD=
 BC=4.
BC=4.在Rt△ABD中,由勾股定理,得
AD=
 =
= =3,
=3,∴S△ABC=
 BC•AD=
BC•AD= ×4×3=6,即等腰三角形ABC的面积是6.
×4×3=6,即等腰三角形ABC的面积是6.分析:通过解方程和三角形的三边关系求得AB=5.如图,过点A作AD⊥BC于点D.则BD=
 BC=4.在Rt△ABD中由勾股定理求得AD=3,S△ABC=
BC=4.在Rt△ABD中由勾股定理求得AD=3,S△ABC= BC•AD=6.
BC•AD=6.点评:本题考查了勾股定理、三角形三边关系以及等腰三角形的性质.正确求得AB边的长度是解题的难点.

练习册系列答案
相关题目
 11、在△ABC中AB=AC,D是AC上的一点,E是AB上的一点,若∠DBC=2∠ABD,添加一个条件
11、在△ABC中AB=AC,D是AC上的一点,E是AB上的一点,若∠DBC=2∠ABD,添加一个条件 7、如图,已知△ABC,AB=AC,AD是中线,E为∠ABD内任一点.
7、如图,已知△ABC,AB=AC,AD是中线,E为∠ABD内任一点.
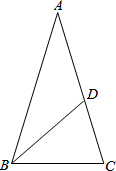 如图,已知△ABC,AB=AC,∠A=36°,∠ABC的平分线BD交AC于点D,
如图,已知△ABC,AB=AC,∠A=36°,∠ABC的平分线BD交AC于点D,