题目内容
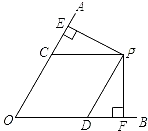
 如图,点P是∠AOB平分线上的一点,过点P作PC∥OA交OB于点C,若∠AOB=30°,OC=4,求点P到OA的距离PD.
如图,点P是∠AOB平分线上的一点,过点P作PC∥OA交OB于点C,若∠AOB=30°,OC=4,求点P到OA的距离PD.分析:过P作PE⊥OB,根据角平分线的性质可得∠AOP=∠POB,PD=PE,再根据平行线证出PC=CO=4,再根据直角三角形的性质可得PE=
PC=2,进而得到PD=2.
| 1 |
| 2 |
解答: 解:过P作PE⊥OB,
解:过P作PE⊥OB,
∵PC∥OA,
∴∠PCB=∠AOB=30°,∠AOP=∠OPC,
∵点P是∠AOB平分线上的一点,
∴∠AOP=∠POB,PD=PE,
∴∠POB=∠OPC,
∴CO=PC,
∵OC=4,
∴PC=4,
∵∠PCB=30°,
∴PE=
PC=2,
∴PD=2.
 解:过P作PE⊥OB,
解:过P作PE⊥OB,∵PC∥OA,
∴∠PCB=∠AOB=30°,∠AOP=∠OPC,
∵点P是∠AOB平分线上的一点,
∴∠AOP=∠POB,PD=PE,
∴∠POB=∠OPC,
∴CO=PC,
∵OC=4,
∴PC=4,
∵∠PCB=30°,
∴PE=
| 1 |
| 2 |
∴PD=2.
点评:此题主要考查了直角三角形的性质,以及角平分线的性质,含30度角的直角三角形的性质:在直角三角形中,30°角所对的直角边等于斜边的一半.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目
 63、如图,点P是∠AOB的平分线上的一点,作PD⊥OA,垂足为D,PE⊥OB垂足为E,DE交OC于点F.则在图中:
63、如图,点P是∠AOB的平分线上的一点,作PD⊥OA,垂足为D,PE⊥OB垂足为E,DE交OC于点F.则在图中: 24、如图,点E是∠AOB的平分线上一点,EC⊥OA,ED⊥OB,垂足分别为C、D.
24、如图,点E是∠AOB的平分线上一点,EC⊥OA,ED⊥OB,垂足分别为C、D.
 PF⊥OB,垂足分别为点E、F.
PF⊥OB,垂足分别为点E、F. 如图,点P是∠AOB内部一点,点P关于OA、OB的对称点是H、G,直线HG交OA、OB于点C、D,若HG=4cm,且∠AOB=30°,则△HOG的周长是
如图,点P是∠AOB内部一点,点P关于OA、OB的对称点是H、G,直线HG交OA、OB于点C、D,若HG=4cm,且∠AOB=30°,则△HOG的周长是