Question

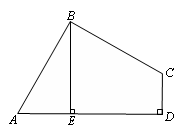
已知：如图，在四边形ABCD中，∠ABC＝90°，CD⊥AD，AD²＋CD²＝2AB²．

（1）求证：AB＝BC；

（2）当BE⊥AD于E时，试证明：BE＝AE＋CD．

 

Answer 1

【答案】

（1）（2）证明见解析

【解析】解：（1）证明：连接AC。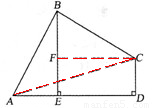

∵∠ABC＝90°，∴AB²＋BC²＝AC²。

∵CD⊥AD，∴AD²＋CD²＝AC²。

∵AD²＋CD²＝2AB²，∴AB²＋BC²＝2AB²。

∴AB＝BC。

（2）证明：过C作CF⊥BE于F。

∵BE⊥AD，∴四边形CDEF是矩形。∴CD＝EF。

∵∠ABE＋∠BAE＝90°，∠ABE＋∠CBF＝90°，∴∠BAE＝∠CBF。

又∵AB＝BC，∠BEA＝∠CFB，∴△BAE≌△CBF（AAS）。∴AE＝BF。

∴BE＝BF＋EF ＝AE＋CD。

（1）题目中存在直角，垂直，含线段平方的等式，因此考虑连接AC，构造直角三角形，利用勾股定理证明。

（2）可采用“截长”法证明，过点C作CF⊥BE于F，易证CD=EF，只需再证明AE=BF即可，这一点又可通过全等三角形获证.