题目内容
3.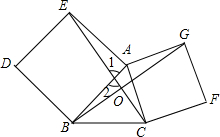 如图,已知锐角△ABC中,以AB,AC为边向外作正方形ABDE和正方形ACFG,连结CE、BG,交点为O,求证:(1)EC=BG;(2)EC⊥BG.
如图,已知锐角△ABC中,以AB,AC为边向外作正方形ABDE和正方形ACFG,连结CE、BG,交点为O,求证:(1)EC=BG;(2)EC⊥BG.
分析 (1)根据正方形的性质易证∠EAC=∠BAG,即可证明△EAC≌△BAG,可得CE=BG;
(2)由△EAC≌△BAG得到∠AEC=∠ABG,即可证明CE⊥BG;
解答 解:(1)在正方形ABDE和正方形ACFG中,AE=AB,AC=AG,
∵∠EAB=∠GAC=90°,
∴∠EAC=∠BAG,
在△EAC和△BAG中,
$\left\{\begin{array}{l}{EA=BA}\\{∠EAC=∠BAG}\\{AC=AG}\end{array}\right.$,
∴△EAC≌△BAG(SAS),
∴CE=BG,
(2)∵△EAC≌△BAG,
∴∠AEC=ABG,
∵∠AEC+∠1=90°,∠1=∠2,
∴∠2+∠ABG=90°,
∴∠BOE=180°-(∠2+∠ABG)=90°,
∴CE⊥BG.
点评 本题考查了全等三角形的判定,考查了全等三角形对应边、对应角相等的性质,本题中求证△EAC≌△BAG是解题的关键.

练习册系列答案
 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
19.为了了解某区5500名初三学生的体重情况,随机抽测了400名学生的体重,统计结果列表如下:
那么样本中体重在50-55范围内的频率是0.21.
| 体重(千克) | 频数 | 频率 |
| 40-45 | 44 | |
| 45-50 | 66 | |
| 50-55 | 84 | |
| 55-60 | 86 | |
| 60-65 | 72 | |
| 65-70 | 48 |
15.三角形的三条边分别为a-1,a,a+1,则a的取值范围是( )
| A. | a>0 | B. | a>2 | C. | 1<a<3 | D. | a>3 |
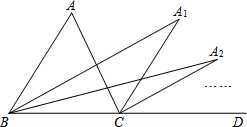 如图,∠ACD是△ABC的外角,∠ABC的平分线与∠ACD的平分线交于点A1,∠A1BC的平分线与∠A1CD的平分线交于点A2,…∠An-1BC的平行线与∠An-1CD的平分线交于点An,设∠A=θ,则∠An=$\frac{θ}{{2}^{n}}$.
如图,∠ACD是△ABC的外角,∠ABC的平分线与∠ACD的平分线交于点A1,∠A1BC的平分线与∠A1CD的平分线交于点A2,…∠An-1BC的平行线与∠An-1CD的平分线交于点An,设∠A=θ,则∠An=$\frac{θ}{{2}^{n}}$.
 如图,圆锥的底面半径为6cm,高为8cm,那么这个圆锥的母线l是10cm.
如图,圆锥的底面半径为6cm,高为8cm,那么这个圆锥的母线l是10cm.