题目内容
已知实数x、y满足x2+ y=
y= ,y2+
,y2+ x=
x= ,且x≠y,则:
,且x≠y,则: +
+ 的值是________.
的值是________.
2+2
分析:把两式相减,运用分解因式法求x+y的值;把①×x-②×y可求xy的值.
把所求式子变形成含有x+y、xy的形式计算求解.
解答:两式相减,得
(x2-y2)+ (y-x)=0,
(y-x)=0,
(x+y)(x-y)- (x-y)=0,
(x-y)=0,
(x-y)(x+y- )=0,
)=0,
∵x≠y,
∴x-y≠0,
∴x+y= ,
,
x2+ y=
y= ①,y2+
①,y2+ x=
x= ②,
②,
①×x-②×y得 x3-y3= (x-y),
(x-y),
∴x2+xy+y2= ,
,
(x+y)2-xy= ,
,
∴xy=2- .
.
 +
+ =
=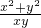 =
= =
=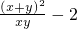 ,
,
= -2=2(2+
-2=2(2+ )-2,
)-2,
=2+2 .
.
点评:此题考查乘法公式的变形运用,难度较大.

分析:把两式相减,运用分解因式法求x+y的值;把①×x-②×y可求xy的值.
把所求式子变形成含有x+y、xy的形式计算求解.
解答:两式相减,得
(x2-y2)+
 (y-x)=0,
(y-x)=0,(x+y)(x-y)-
 (x-y)=0,
(x-y)=0,(x-y)(x+y-
 )=0,
)=0,∵x≠y,
∴x-y≠0,
∴x+y=
 ,
,x2+
 y=
y= ①,y2+
①,y2+ x=
x= ②,
②,①×x-②×y得 x3-y3=
 (x-y),
(x-y),∴x2+xy+y2=
 ,
,(x+y)2-xy=
 ,
,∴xy=2-
 .
. +
+ =
=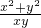 =
= =
=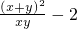 ,
,=
 -2=2(2+
-2=2(2+ )-2,
)-2,=2+2
 .
.点评:此题考查乘法公式的变形运用,难度较大.

练习册系列答案
相关题目
已知实数a、b满足a<b,则下列式子中正确的是( )
A、
| ||||
| B、b-a>0 | ||||
| C、a2<b2 | ||||
| D、a4<b4 |