题目内容
 如图,反比例函数y=
如图,反比例函数y= (k<0)的图象经过点A(-
(k<0)的图象经过点A(- ,m),过A作AB⊥x轴于点B,△AOB的面积为
,m),过A作AB⊥x轴于点B,△AOB的面积为 .
.
(1)求k和m的值;
(2)若过A点的直线y=ax+b与x轴交于C点,且∠ACO=30°,求此直线的解析式.
解:(1)S△AOB= •OB•AB=
•OB•AB= ×
× •m=
•m=
∴m=2,A(- ,2)
,2)
∵反比例函数y= (k<0)的图象经过点A
(k<0)的图象经过点A
∴k=-2 ;
;
(2)分类讨论:
①C点在负半轴.在△ABC中,AB=2,∠C=30°,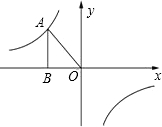
∴BC=2 ,C(-3
,C(-3 ,0);
,0);
解方程组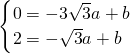 得
得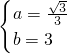 ,
,
所以直线解析式为y= x+3.
x+3.
②C点在正半轴.在△ABC中,AB=2,∠C=30°,
∴BC=2 ,C(
,C( ,0);
,0);
解方程组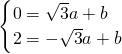 得,
得,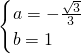 ,
,
所以满足条件的直线解析式为y=- x+1.
x+1.
综上所述,所以满足条件的直线解析式为y= x+3和y=-
x+3和y=- x+1.
x+1.
分析:(1)根据面积求m,再根据A点坐标求k;
(2)因为要满足∠ACO=30°这个条件,所以必须分类讨论:C点在负半轴、C点在正半轴.求C点坐标后再求直线解析式.
点评:此题中C点位置没有明确,需根据题意分情况探索,所以需分类讨论.分类讨论的思想训练学生思维的严密性.
 •OB•AB=
•OB•AB= ×
× •m=
•m=
∴m=2,A(-
 ,2)
,2)∵反比例函数y=
 (k<0)的图象经过点A
(k<0)的图象经过点A∴k=-2
 ;
;(2)分类讨论:
①C点在负半轴.在△ABC中,AB=2,∠C=30°,

∴BC=2
 ,C(-3
,C(-3 ,0);
,0);解方程组
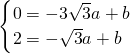 得
得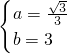 ,
,所以直线解析式为y=
 x+3.
x+3.②C点在正半轴.在△ABC中,AB=2,∠C=30°,
∴BC=2
 ,C(
,C( ,0);
,0);解方程组
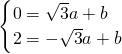 得,
得,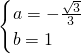 ,
,所以满足条件的直线解析式为y=-
 x+1.
x+1.综上所述,所以满足条件的直线解析式为y=
 x+3和y=-
x+3和y=- x+1.
x+1.分析:(1)根据面积求m,再根据A点坐标求k;
(2)因为要满足∠ACO=30°这个条件,所以必须分类讨论:C点在负半轴、C点在正半轴.求C点坐标后再求直线解析式.
点评:此题中C点位置没有明确,需根据题意分情况探索,所以需分类讨论.分类讨论的思想训练学生思维的严密性.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图,反比例函数y=
如图,反比例函数y= 如图,反比例函数
如图,反比例函数 如图,反比例函数
如图,反比例函数 如图,反比例函数
如图,反比例函数 如图,反比例函数
如图,反比例函数