题目内容
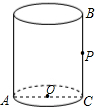如图，圆柱的底面周长为6cm，AC是底面圆的直径，高BC=6cm，点P是每线BC上一点且PC=
BC．一只蚂蚁从点A出发沿着圆柱体的表面爬行到点P的最短距离是________．
5cm
分析：首先画出圆柱的侧面展开图，根据高BC′=6cm，PC=BC，求出PC′=×6=4cm，在Rt△AC′P中，根据勾股定理求出AP的长．
解答：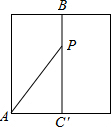
解：侧面展开图如图所示，
∵圆柱的底面周长为6cm，
∴AC′=3cm，
∵PC′=BC′，
∴PC′=×6=4cm，
在Rt△ACP中，
AP2=AC′2+CP2，
∴AP=
=5．
故答案为：5cm．
点评：此题主要考查了平面展开图，以及勾股定理的应用，做题的关键是画出圆柱的侧面展开图．
分析：首先画出圆柱的侧面展开图，根据高BC′=6cm，PC=
BC，求出PC′=×6=4cm，在Rt△AC′P中，根据勾股定理求出AP的长．解答：
解：侧面展开图如图所示，∵圆柱的底面周长为6cm，
∴AC′=3cm，
∵PC′=
BC′，∴PC′=
×6=4cm，在Rt△ACP中，
AP2=AC′2+CP2，
∴AP=
=5．故答案为：5cm．
点评：此题主要考查了平面展开图，以及勾股定理的应用，做题的关键是画出圆柱的侧面展开图．
练习册系列答案
相关题目
如图，圆柱的底面周长为6cm，AC是底面圆的直径，高BC=6cm，点P是母线BC上一点，且PC=| 2 |
| 3 |
A、(4+
| ||
| B、5cm | ||
C、3
| ||
| D、7cm |
如图，圆柱的底面周长为12cm，AC是底面圆的直径，高BC=10cm，点P是BC上一点且PC=| 4 |
| 5 |
| A、9cm | B、10cm |
| C、11cm | D、12cm |
BC．一只蚂蚁从A点出发沿着圆柱体的表面爬行到点P的最短距离是（ ）
㎝ 
㎝