题目内容
 如图,已知CD是△ABC的角平分线,AE⊥CD垂足为E,EF∥BC,交AC于F,则EF与
如图,已知CD是△ABC的角平分线,AE⊥CD垂足为E,EF∥BC,交AC于F,则EF与| 1 |
| 2 |
A、EF>
| ||
B、EF=
| ||
C、EF<
| ||
| D、不能确定 |
分析:由EF∥BC和CD是△ABC的角平分线,易得EF=CF,而根据等角的余角相等,可得∠4=∠5,则EF=AF,则AF=CF,可得EF=
AC.
| 1 |
| 2 |
解答: 解:∵CD是△ABC的角平分线,
解:∵CD是△ABC的角平分线,
∴∠1=∠2,
∵EF∥BC,
∴∠2=∠3,
∴∠1=∠3,
∴EF=CF,
∵AE⊥CD,
∴∠1+∠5=90°,∠3+∠4=90°,
∴∠4=∠5,
∴EF=AF,
∴AF=CF,
∴EF=
AC.
故选B.
 解:∵CD是△ABC的角平分线,
解:∵CD是△ABC的角平分线,∴∠1=∠2,
∵EF∥BC,
∴∠2=∠3,
∴∠1=∠3,
∴EF=CF,
∵AE⊥CD,
∴∠1+∠5=90°,∠3+∠4=90°,
∴∠4=∠5,
∴EF=AF,
∴AF=CF,
∴EF=
| 1 |
| 2 |
故选B.
点评:此题主要考查角平分线的定义和平行线的性质以及直角三角形的有关性质和等角对等边等知识点,要合理利用已知条件,难度中等.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目
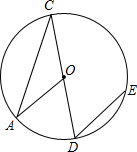 如图,已知CD是⊙O的直径,过点D的弦DE平行于半径OA,若∠D的度数是50°,则∠C的度数是( )
如图,已知CD是⊙O的直径,过点D的弦DE平行于半径OA,若∠D的度数是50°,则∠C的度数是( )| A、25° | B、30° | C、40° | D、50° |
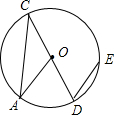 如图,已知CD是⊙O的直径,弦DE∥半径OA,∠D=50°,∠C=( )
如图,已知CD是⊙O的直径,弦DE∥半径OA,∠D=50°,∠C=( )| A、50° | B、40° | C、25° | D、20° |
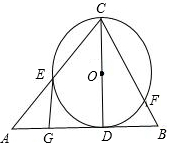 如图,已知CD是△ABC中AB边上的高,以CD为直径的⊙O交CA于点E,点G是AD的中点.
如图,已知CD是△ABC中AB边上的高,以CD为直径的⊙O交CA于点E,点G是AD的中点.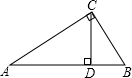 如图,已知CD是Rt△ABC的斜边上的高,其中AD=9cm,BD=4cm,那么CD等于
如图,已知CD是Rt△ABC的斜边上的高,其中AD=9cm,BD=4cm,那么CD等于 (2012•苍梧县二模)如图,已知CD是⊙O的直径,AC⊥CD,垂足为C,弦DE∥OA,直线AE,CD相交于点B.
(2012•苍梧县二模)如图,已知CD是⊙O的直径,AC⊥CD,垂足为C,弦DE∥OA,直线AE,CD相交于点B.