题目内容
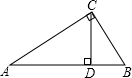如图，已知CD是Rt△ABC的斜边上的高，其中AD=9cm，BD=4cm，那么CD等于分析：利用△ACD∽△CBD，对应线段成比例就可以求出．
解答：解：∵CD⊥AB，∠ACB=90°
∴△ACD∽△CBD，
∴
=
，
∴
=
，
∴CD=6．
∴△ACD∽△CBD，
∴
| CD |
| AD |
| BD |
| CD |
∴
| CD |
| 9 |
| 4 |
| CD |
∴CD=6．
点评：本题关键在于从相似三角形中找对应比例线段，由相似三角形对应线段成比例来解题．
练习册系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
如图，已知CD是Rt△ABC斜边上的高，AC=4，BC=3，计算cos∠BCD的值．
如图，已知CD是Rt△ABC斜边上的高，AD=3，BD=8则CD的长为（ ）
如图，已知CD是Rt△ABC的斜边AB上的高，其中AD=6，BD=4，那么CD=
C.
24 D.
5 