题目内容
2.下列事件是必然事件的是( )| A. | 任意购买一张电影票,座位号是奇数 | |
| B. | 打开电视,正在播出“奔跑吧,兄弟” | |
| C. | 13名同学中至少有两名同学出生的月份相同 | |
| D. | 抛掷一枚硬币,反面朝上 |
分析 根据事件发生的可能性大小判断相应事件的类型即可.
解答 解:A、任意购买一张电影票,座位号是奇数是随机事件,故A不符合题意;
B、打开电视,正在播出“奔跑吧,兄弟”是随机事件,故B不符合题意;
C、13名同学中至少有两名同学出生的月份相同是必然事件,故C符合题意;
D、抛掷一枚硬币,反面朝上是随机事件,故D不符合题意;
故选:C.
点评 本题考查的是必然事件、不可能事件、随机事件的概念.必然事件指在一定条件下,一定发生的事件.不可能事件是指在一定条件下,一定不发生的事件,不确定事件即随机事件是指在一定条件下,可能发生也可能不发生的事件.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
13.计算4$\sqrt{3+2\sqrt{2}}$-$\sqrt{41+24\sqrt{2}}$=( )
| A. | $\sqrt{2}-1$ | B. | 1 | C. | $\sqrt{2}$ | D. | 2 |
10.若-1<x<0,则x,x2,x3的大小关系是( )
| A. | x<x3<x2 | B. | x<x2<x3 | C. | x3<x<x2 | D. | x2<x3<x |
17.下列运算正确的是( )
| A. | 2a+3b=5ab | B. | a2•a3=a5 | C. | (2a)3=6a 3 | D. | a6+a3=a9 |
7.下列实数中是有理数的是( )
| A. | $\sqrt{3}$ | B. | $\root{3}{2}$ | C. | π | D. | π0 |
14.若|a-1|+(b+3)2=0,则ba=( )
| A. | -3 | B. | -1 | C. | 3 | D. | 1 |
11.把所有正奇数从小到大排列,并按如下规律分组:(1),(3,5,7),(9,11,13,15,17),(19,21,23,25,27,29,31),…,现有等式Am=(i,j)表示正奇数m是第i组第j个数(从左往右数),如A7=(2,3),A9=(3,1),则A2015=( )
| A. | (31,50) | B. | (32,47) | C. | (33,46) | D. | (34,42) |
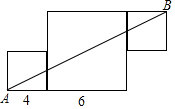 如图,由三个正方形组成一个图形,其中来个正方形的边长分别为4,6,若线段AB将这个圆形分成面积相等的两部分,则第三个正方形的边长为2或4.
如图,由三个正方形组成一个图形,其中来个正方形的边长分别为4,6,若线段AB将这个圆形分成面积相等的两部分,则第三个正方形的边长为2或4.