题目内容
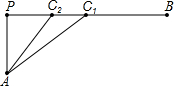
如图，线段AP⊥PB，而且AP=2，PB=12，点C1，C2在线段PB上，满足PC2=1.5，BC1=6．设m=
+
，n=
+
，那么（ ）
| AC2 |
| 3 |
| C2B |
| 5 |
| AC1 |
| 3 |
| C1B |
| 5 |
| A．m＞n | B．m=n | C．m+n=5 | D．m＜n |
∵线段AP⊥PB，且AP=2，PB=12，PC2=1.5，BC1=6．
故根据勾股定理可求出：AC2=2.5，BC2=10.5，AC1=2
，BC1=6．
∴m=
+
=
＜n=
+
=
．
故选D．
故根据勾股定理可求出：AC2=2.5，BC2=10.5，AC1=2
| 10 |
∴m=
| 2.5 |
| 3 |
| 10.5 |
| 5 |
| 44 |
| 15 |
2
| ||
| 3 |
| 6 |
| 5 |
20
| ||
| 15 |
故选D．
练习册系列答案
相关题目
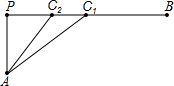如图，线段AP⊥PB，而且AP=2，PB=12，点C1，C2在线段PB上，满足PC2=1.5，BC1=6．设m=| AC2 |
| 3 |
| C2B |
| 5 |
| AC1 |
| 3 |
| C1B |
| 5 |
| A、m＞n | B、m=n |
| C、m+n=5 | D、m＜n |
18、如图，PA、PB分别切⊙O于A、B，根据这些条件，你能得出哪些结论？（不再添字母和线段，半径相等除外，只写3个正确结论即可）
如图，线段AP⊥PB，而且AP=2，PB=12，点C1，C2在线段PB上，满足PC2=1.5，BC1=6．设
，那么
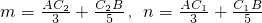，那么（ ）