Question

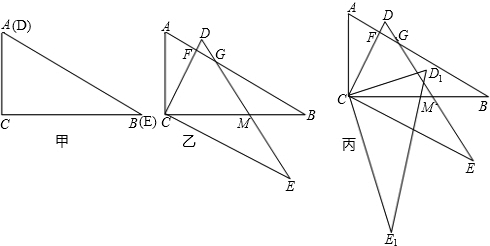
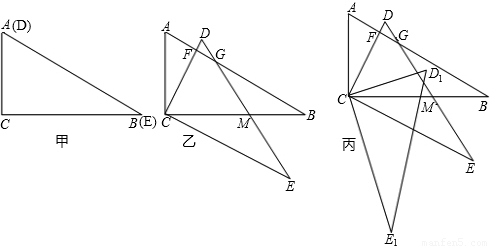
如图，把Rt△ACB与Rt△DCE按图（甲）所示重叠在一起，其中AC=2，∠BAC=60°，若把Rt△DCE绕直角顶点C按顺时针方向旋转30°，使得AB分别与DC，DE相交于点F、G，CB与DE相交于点M，如图（乙）所示．
（1）求CM的长；
（2）求△ACB与△DCE的重叠部分（即四边形CMGF）的面积（保留根号）；
（3）将△DCE按顺时针方向继续旋转45°，得△D₁CE₁，这时，点D₁在△ACB的内部，外部，还是边上？证明你的判断．

Answer 1

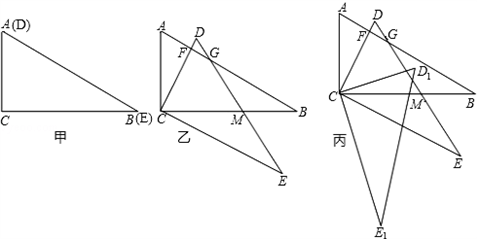
解：（1）∵旋转角度为30°，即∠ACD=30°，
∴∠DCM=90°﹣30°=60°，
∴∠D=∠DCM=60°，
∴△DCM为正三角形，
∴CM=CD=2；
（2）在△ACF中，∠AFC=180°﹣∠BAC﹣∠ACD=180°﹣60°﹣30°=90°，
∵AC=2，
∴CF=ACsin60°=2×=，DF=CD﹣CF=2﹣，
在Rt△DFG中，FG=DFtan60°=（2﹣），
由图可知S_{四边形CMGF}=S_△DCM﹣S_△DFG，
=×2×（2×）﹣×（2﹣）×（2﹣），
=﹣（7﹣12），
=6﹣；
（3）点D₁在△ACB的内部．
理由如下：如图，设直线CD与直线AB相交于点N，
∵△DCE按顺时针方向继续旋转45°，
∴∠FCN=45°，在Rt△FCN中，CN=CF÷cos∠FCN=÷=，
∵＞2，
∴点D₁在△ACB的内部．