Question

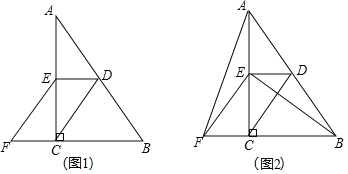
【题目】如图，在Rt△ABC中，∠ACB=90°，BC=6，AC=8，分别以点A，B为圆心，大于线段AB长度一半的长为半径作弧，相交于点E，F，过点E，F作直线EF，交AB于点D，连结CD，则CD的长是 ．

Answer 1

【答案】5
【解析】解：由题意EF是线段AB的垂直平分线，
∴AD=DB，
Rt△ABC中，∵∠ACB=90°，BC=6，AC=8，
∴AB= = =10，
∵AD=DB，∠ACB=90°，
∴CD= AB=5．
所以答案是5．

【考点精析】解答此题的关键在于理解直角三角形斜边上的中线的相关知识，掌握直角三角形斜边上的中线等于斜边的一半，以及对勾股定理的概念的理解，了解直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2．