题目内容
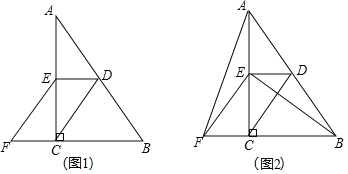
【题目】已知：如图，在
中，
，点D、E分别是AB、AC的中点，点F在BC延长线上，连接EF，且
．
如图1，求证：四边形CDEF是平行四边形；
如图2，连接AF、BE，在不添加任何辅助线的情况下，请直接写出图2中所有与
面积相等的三角形．
【答案】
证明见解析； 
与
面积相等的三角形有：
，
，
，
．
【解析】
（1）根据三角形中位线性质得
，根据直角三角形斜边上中线性质得
，再证
，得
，可证四边形CDEF是平行四边形．（2）由（1）可知有关相等的线段，根据三角形的面积公式进行分析即可.
证明：
点D、E分别是AB、AC的中点，
是
的中位线，
，
，
，
，
，
，
，
，
四边形CDEF是平行四边形．
如图2中，与面积相等的三角形有：，，，．
理由：四边形CDEF是平行四边形，
与
的面积相等，
，，
与，与的面积相等，
与面积相等的三角形有：，，，．
练习册系列答案
相关题目
