题目内容
5.已知方程x2-2x-8=0.解决以下问题:(1)不解方程试判断此方程的根的情况.
(2)请按要求分别解这个方程:①配方法;②因式分解法.
(3)①这些方法都是将解一元二次方程转化为解一元一次方程,以达到将方程降次的目的;
②尝试解方程:x3+2x2-3x=0.
分析 (1)由根的判别式△=b2-4ac=36,可判断出此方程有两个不相等的实数根;
(2)①按照配方法解方程的步骤一步步解方程;②按照分解因式法解方程的步骤一步步解方程;
(3)①解方程的方法都是达到降次的目的,故可出结论;②利用分解因式解方程的方法一步步解决方程.
解答 解:(1)∵a=1,b=-2,c=-8,
∴△=b2-4ac=(-2)2-4×1×(-8)=36>0,
∴此方程有两个不相等的实数根.
(2)①配方法:x2-2x-8=0,
配方,得(x-1)2=9,
方程两边开方,得x-1=±3,
解得:x1=4,x2=-2;
②因式分解法:x2-2x-8=0,
分解因式,得(x-4)(x+2)=0,
解得::x1=4,x2=-2.
(3)①这些方法都是将解一元二次方程转化为解一元一次方程,以达到将方程降次的目的.
故答案为:一元二次;一元一次.
②x3+2x2-3x=0,
提取公因式x,得x(x2+2x-3)=0,
分解因式,得x(x+3)(x-1)=0,
解得:x1=0,x2=-3,x3=1.
点评 本题考查了根的判别式、配方法解一元二次方程以及因式分解法解一元二次方程,解题的关键:①明白根的判别式的意义;(2)能够熟练的运用各种解方程的方法;(3)明白解方程过程的意义.本题属于基础题,难度不大,解方程是中考必考内容之一,这就要求学生能够很好的掌握各种解方程的方法.

练习册系列答案
相关题目
13.下列各式中,是关于x,y的二元一次方程的是( )
| A. | 2x-y | B. | x-3y=-15 | C. | xy+x-2=0 | D. | $\frac{2}{x}$-y=0 |
20.根据下列表格中关于x的代数式ax2+bx+c的值与x的对应值,判断方程ax2+bx+c=0(a≠0,a,b,c为常数)的一个解的范围是( )
| x | 5.12 | 5.13 | 5.14 | 5.15 |
| ax2+bx+c | -0.04 | -0.02 | 0.01 | 0.03 |
| A. | 5.14<x<5.15 | B. | 5.13<x<5.14 | C. | 5.12<x<5.13 | D. | 5.10<x<5.12 |
10.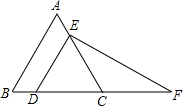 如图,在等边三角形ABC中,点D,E分别在边BC,AC上,DE∥AB,过点E作EF⊥DE,交BC的延长线于点F;若△CEF一边的长为2,则△CEF的周长为( )
如图,在等边三角形ABC中,点D,E分别在边BC,AC上,DE∥AB,过点E作EF⊥DE,交BC的延长线于点F;若△CEF一边的长为2,则△CEF的周长为( )
 如图,在等边三角形ABC中,点D,E分别在边BC,AC上,DE∥AB,过点E作EF⊥DE,交BC的延长线于点F;若△CEF一边的长为2,则△CEF的周长为( )
如图,在等边三角形ABC中,点D,E分别在边BC,AC上,DE∥AB,过点E作EF⊥DE,交BC的延长线于点F;若△CEF一边的长为2,则△CEF的周长为( )| A. | 4+2$\sqrt{3}$ | B. | 4+2$\sqrt{3}$或2+$\frac{4}{3}$$\sqrt{3}$ | C. | 2+2$\sqrt{3}$或2+$\frac{4}{3}$$\sqrt{3}$ | D. | 4+2$\sqrt{3}$或2+$\frac{2}{3}$$\sqrt{3}$ |