题目内容
如图, 的三边长分别为
的三边长分别为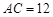 ,
,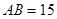 ,
,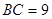 .若将
.若将 沿线段
沿线段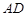 折叠,点
折叠,点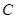 正好落在
正好落在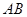 边上的点
边上的点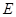 处.求线段
处.求线段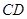 的长度.
的长度.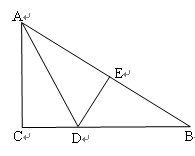
设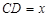 ,则
,则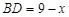 ……………………………(1分)
……………………………(1分)
∵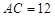 ,
,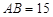 ,
,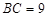
∴
∴ …………………………………………(4分)
…………………………………………(4分)
∵将 沿
沿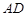 折叠,点
折叠,点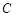 与点
与点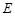 重合
重合
∴ ,
,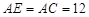

∴

∵在Rt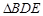 中,
中,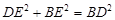 ………………(7分)
………………(7分)
∴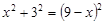 ……………………………………(8分)
……………………………………(8分)
解得
∴ ………………………………………………(9分)
………………………………………………(9分)
解析试题分析:设CD=x,则根据折叠的性质可得出AE=AC=9,EB=6,BD=12-x,在RT△CDB中可求出x的值.
考点:翻折变换(折叠问题).
点评:此题要求熟练掌握翻折变换及勾股定理的知识,求出CD的长度.

练习册系列答案
相关题目
 的三条中位线又组成了一个小三角形.
的三条中位线又组成了一个小三角形.
 )拼成一个六边形,由于大六边形三个角都是∠B+∠C=120°,所以由a边围成了一个大的正六边形,其面积可计算出为 ;由于所围成的小六边形的边长都是 ,其面积为 ,由此可得
)拼成一个六边形,由于大六边形三个角都是∠B+∠C=120°,所以由a边围成了一个大的正六边形,其面积可计算出为 ;由于所围成的小六边形的边长都是 ,其面积为 ,由此可得 ),先画出这个正三角形,再推出
),先画出这个正三角形,再推出 边形吗?如果能,试写出∠A和三角形的面积
边形吗?如果能,试写出∠A和三角形的面积 的表达式;如果不能,请简要说明理由.
的表达式;如果不能,请简要说明理由.
 的三边长分别为
的三边长分别为 ,
, ,
, .若将
.若将 折叠,点
折叠,点 正好落在
正好落在 边上的点
边上的点 处.求线段
处.求线段 的长度.
的长度.
 )拼成一个六边形,由于大六边形三个角都是∠B+∠C=120°,所以由a边围成了一个大的正六边形,其面积可计算出为 ;由于所围成的小六边形的边长都是 ,其面积为 ,由此可得
)拼成一个六边形,由于大六边形三个角都是∠B+∠C=120°,所以由a边围成了一个大的正六边形,其面积可计算出为 ;由于所围成的小六边形的边长都是 ,其面积为 ,由此可得 ),先画出这个正三角形,再推出
),先画出这个正三角形,再推出 边形吗?如果能,试写出∠A和三角形的面积
边形吗?如果能,试写出∠A和三角形的面积 的表达式;如果不能,请简要说明理由.
的表达式;如果不能,请简要说明理由.