题目内容
已知:如图△ABC的三边长分别为a、b、c,它的三条中位线组成一个新的三角形,这个新三角形 的三条中位线又组成了一个小三角形.
的三条中位线又组成了一个小三角形.(1)求这个小三角形的周长.
(2)照上述方法继续做下去,到第n次时,这个小三角形的周长是多少?
分析:(1)根据中位线的性质可以得到这个小三角形与原来的三角形相似,且相似比为
,根据相似三角形周长的比等于相似比能求出这个小三角形的周长.(2)按照这种方法作出的三角形与原来的三角形相似,相似比为
,所以第n个小三角形的周长是第一个三角形周长的
.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2n |
解答:解:(1)因为这个新三角形的三边分别与原三角形的三边平行,所以新三角形与原三角形相似,根据中位线的性质可知,两三角形的相似比是
,因此,这个小三角形的周长为
(a+b+c);
(2)由于第一个三角形的周长为
(a+b+c),第二个小三角形的周长为
(a+b+c)=
(a+b+c).
依此类推可得第n个小三角形的周长为
(a+b+c).
| 1 |
| 2 |
| 1 |
| 4 |
(2)由于第一个三角形的周长为
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 22 |
依此类推可得第n个小三角形的周长为
| 1 |
| 2n |
点评:本题考查的是相似三角形的判定与性质,(1)根据三角形的中位线得到新三角形与原来的三角形相似,并且相似比为
,利用相似三角形周长的比等于相似比,求出第一个新三角形的周长.(2)根据第二个三角形的周长进行分析,寻找规律,得到第n个三角形的周长.
| 1 |
| 2 |

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目
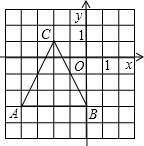 已知:如图△ABC的顶点坐标分别为A(-4,-3),B(0,-3),C(-2,1),如将B点向右平移2个单位后再向上平移4个单位到达B1点,若设△ABC的面积为S1,△AB1C的面积为S2,则S1,S2的大小关系为( )
已知:如图△ABC的顶点坐标分别为A(-4,-3),B(0,-3),C(-2,1),如将B点向右平移2个单位后再向上平移4个单位到达B1点,若设△ABC的面积为S1,△AB1C的面积为S2,则S1,S2的大小关系为( )| A、S1>S2 | B、S1=S2 | C、S1<S2 | D、不能确定 |
 已知:如图△ABC的顶点坐标分别为A(-4,-3),B(0,-3),C(-2,1),如将B点向右平移2个单位后再向上平移4个单位到达B1点,若设△ABC的面积为S1,△AB1C的面积为S2,则S1,S2的大小关系为s1
已知:如图△ABC的顶点坐标分别为A(-4,-3),B(0,-3),C(-2,1),如将B点向右平移2个单位后再向上平移4个单位到达B1点,若设△ABC的面积为S1,△AB1C的面积为S2,则S1,S2的大小关系为s1 22、已知:如图△ABC的顶点坐标分别为A(-4,-3),B(0,-3),C(-2,1),如将B点向右平移2个单位后再向上平移4个单位到达B1点,若设△ABC的面积为S1,△AB1C的面积为S2.
22、已知:如图△ABC的顶点坐标分别为A(-4,-3),B(0,-3),C(-2,1),如将B点向右平移2个单位后再向上平移4个单位到达B1点,若设△ABC的面积为S1,△AB1C的面积为S2.