题目内容
如图。矩形ABCD的对角线AC、BD相交于点0,过点O作OE⊥AC交AB于E,若BC=4,△AOE的面积为5,则sin∠BOE的值为 .

考点:线段垂直平分线的性质;勾股定理;矩形的性质。解直角三角形
分析:本题利用三角形的面积计算此题考查了矩形的性质、垂直平分线的性质以及勾股定理及解直角三角形.注意数形结合思想的应用,此题综合性较强,难度较大,
解答:由△AOE的面积为5,找此三角形的高,作OH⊥AE于E,得OH∥BC,AH=BH,由三角形的中位线∵BC=4 ∴OH=2,从而AE=5,连接CE,
由AO=OC, OE⊥AC得EO是AC的垂直平分线,∴AE=CE,在直角三角形EBC中,BC=4,AE=5, 勾股定理得EB=3,AB=8,在直角三角形ABC中,勾股定理得AC=![]()
,BO=![]() AC=
AC=![]() ,作EM⊥BO于M,在直角三角形EBM中,EM=BEsin∠ABD=3×
,作EM⊥BO于M,在直角三角形EBM中,EM=BEsin∠ABD=3×![]()
=![]() ,BM= BEcos∠ABD=3×
,BM= BEcos∠ABD=3×![]() =
=![]() ,从而OM=
,从而OM=![]() ,在直角三角形E0M中,勾股定理得OE=
,在直角三角形E0M中,勾股定理得OE=![]() ,sin∠BOE=
,sin∠BOE=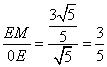

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
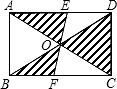 如图,矩形ABCD的对角线AC和BD相交于点O,过点O的直线分别交AD和BC于点E、F,AB=2,BC=3,则图中阴影部分的面积为
如图,矩形ABCD的对角线AC和BD相交于点O,过点O的直线分别交AD和BC于点E、F,AB=2,BC=3,则图中阴影部分的面积为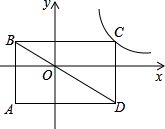 如图,矩形ABCD的对角线BD经过坐标原点,矩形的边分别平行于坐标轴,点C在反比例函数y=
如图,矩形ABCD的对角线BD经过坐标原点,矩形的边分别平行于坐标轴,点C在反比例函数y= 如图,矩形ABCD的一边AD在x轴上,对角线AC、BD交于点E,过B点的双曲线
如图,矩形ABCD的一边AD在x轴上,对角线AC、BD交于点E,过B点的双曲线 (2013•葫芦岛)如图,矩形ABCD的对角线交于点O,∠BOC=60°,AD=3,动点P从点A出发,沿折线AD-DO以每秒1个单位长的速度运动到点O停止.设运动时间为x秒,y=S△POC,则y与x的函数关系大致为( )
(2013•葫芦岛)如图,矩形ABCD的对角线交于点O,∠BOC=60°,AD=3,动点P从点A出发,沿折线AD-DO以每秒1个单位长的速度运动到点O停止.设运动时间为x秒,y=S△POC,则y与x的函数关系大致为( ) 如图,矩形ABCD的对角线交于O点,∠AOB=120°,AD=5cm,则AC=
如图,矩形ABCD的对角线交于O点,∠AOB=120°,AD=5cm,则AC=